Question Number 12683 by tawa last updated on 29/Apr/17

$$\mathrm{A}\:\mathrm{coil}\:\mathrm{of}\:\mathrm{inductance}\:\mathrm{0}.\mathrm{12Hz}\:\mathrm{and}\:\mathrm{resistance}\:\mathrm{4}\:\Omega\:\mathrm{is}\:\mathrm{connected}\:\mathrm{across}\:\mathrm{a}\:\mathrm{240}\:\mathrm{v},\: \\ $$$$\mathrm{50}\:\mathrm{Hz}\:\mathrm{is}\:\mathrm{supplied}\:.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{current}\:\mathrm{on}\:\mathrm{the}\:\mathrm{load}\:\left(\pi\:=\:\mathrm{3}.\mathrm{142}\right). \\ $$
Answered by ajfour last updated on 29/Apr/17
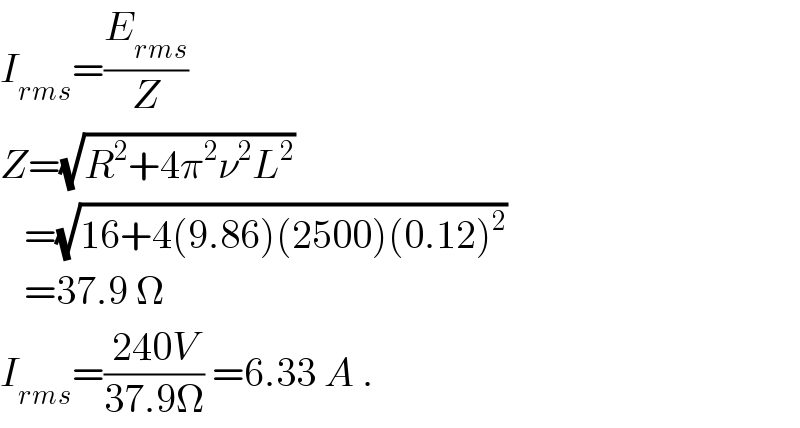
$${I}_{{rms}} =\frac{{E}_{{rms}} }{{Z}} \\ $$$${Z}=\sqrt{{R}^{\mathrm{2}} +\mathrm{4}\pi^{\mathrm{2}} \nu^{\mathrm{2}} {L}^{\mathrm{2}} }\: \\ $$$$\:\:\:=\sqrt{\mathrm{16}+\mathrm{4}\left(\mathrm{9}.\mathrm{86}\right)\left(\mathrm{2500}\right)\left(\mathrm{0}.\mathrm{12}\right)^{\mathrm{2}} }\: \\ $$$$\:\:\:=\mathrm{37}.\mathrm{9}\:\Omega \\ $$$${I}_{{rms}} =\frac{\mathrm{240}{V}}{\mathrm{37}.\mathrm{9}\Omega}\:=\mathrm{6}.\mathrm{33}\:{A}\:. \\ $$
Commented by tawa last updated on 29/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
