Question Number 8972 by tawakalitu last updated on 09/Nov/16

$$\mathrm{A}\:\mathrm{cylindrical}\:\mathrm{can}\:\mathrm{of}\:\mathrm{internal}\:\mathrm{diameter}\:\mathrm{8cm} \\ $$$$\mathrm{contains}\:\mathrm{water}\:\mathrm{to}\:\mathrm{a}\:\mathrm{deep}\:\mathrm{of}\:\mathrm{6cm}.\:\mathrm{24000}\:\mathrm{heavy} \\ $$$$\mathrm{spherical}\:\mathrm{pullet}\:\mathrm{of}\:\mathrm{diameter}\:\mathrm{2mm}\:\mathrm{are}\:\mathrm{dropped} \\ $$$$\mathrm{into}\:\mathrm{the}\:\mathrm{can}.\:\mathrm{how}\:\mathrm{far}\:\mathrm{does}\:\mathrm{the}\:\mathrm{water}\:\mathrm{level}\:\mathrm{rise}\:? \\ $$
Answered by Rasheed Soomro last updated on 09/Nov/16
![Diameter 2mm=Diamter 0.2cm=Radius 0.1cm Volume of sphere of radius r=(4/3)πr^3 Volume of sperical pullet=(4/3)π(0.1cm)^3 =((0.004)/3)π cm^3 Volume of 24000 sperical pullet=24000×((0.004)/3)π cm^3 =32π cm^3 Volume of water before dropping pullets =π(4cm)^2 (6cm)=96π cm^3 [V=πr^2 h] Additional water is ((32π)/(96π))=(1/3)of initial water. So rise of water will be (1/3) of initial height of water in the can. Hence the rise of water is (1/3)×6cm=2cm](https://www.tinkutara.com/question/Q8974.png)
$$\mathrm{Diameter}\:\mathrm{2mm}=\mathrm{Diamter}\:\mathrm{0}.\mathrm{2cm}=\mathrm{Radius}\:\mathrm{0}.\mathrm{1cm}\: \\ $$$$\mathrm{Volume}\:\mathrm{of}\:\mathrm{sphere}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{r}=\frac{\mathrm{4}}{\mathrm{3}}\pi\mathrm{r}^{\mathrm{3}} \\ $$$$\mathrm{Volume}\:\mathrm{of}\:\mathrm{sperical}\:\mathrm{pullet}=\frac{\mathrm{4}}{\mathrm{3}}\pi\left(\mathrm{0}.\mathrm{1cm}\right)^{\mathrm{3}} =\frac{\mathrm{0}.\mathrm{004}}{\mathrm{3}}\pi\:\:\:\mathrm{cm}^{\mathrm{3}} \\ $$$$\mathrm{Volume}\:\mathrm{of}\:\mathrm{24000}\:\mathrm{sperical}\:\mathrm{pullet}=\mathrm{24000}×\frac{\mathrm{0}.\mathrm{004}}{\mathrm{3}}\pi\:\:\:\mathrm{cm}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{32}\pi\:\mathrm{cm}^{\mathrm{3}} \\ $$$$\mathrm{Volume}\:\mathrm{of}\:\mathrm{water}\:\mathrm{before}\:\mathrm{dropping}\:\mathrm{pullets} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi\left(\mathrm{4cm}\right)^{\mathrm{2}} \left(\mathrm{6cm}\right)=\mathrm{96}\pi\:\:\mathrm{cm}^{\mathrm{3}} \:\:\:\:\:\:\:\:\left[\mathrm{V}=\pi\mathrm{r}^{\mathrm{2}} \mathrm{h}\right] \\ $$$$\mathrm{Additional}\:\mathrm{water}\:\mathrm{is}\:\frac{\mathrm{32}\pi}{\mathrm{96}\pi}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{of}\:\mathrm{initial}\:\mathrm{water}. \\ $$$$\mathrm{So}\:\mathrm{rise}\:\mathrm{of}\:\mathrm{water}\:\mathrm{will}\:\mathrm{be}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{of}\:\mathrm{initial}\:\mathrm{height}\:\mathrm{of}\:\mathrm{water} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{can}. \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{rise}\:\mathrm{of}\:\mathrm{water}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{6cm}=\mathrm{2cm} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 09/Nov/16

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 09/Nov/16
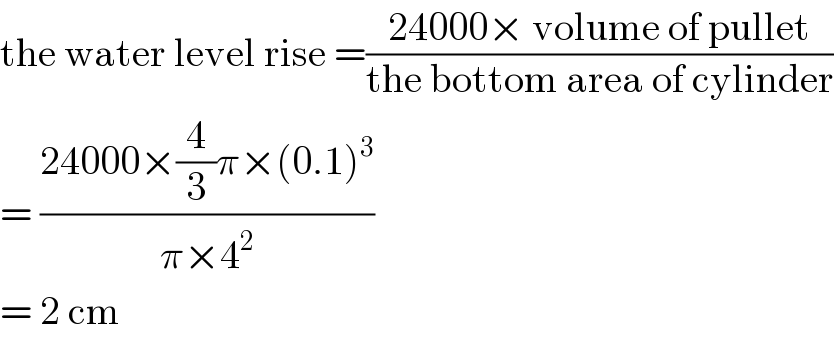
$$\mathrm{the}\:\mathrm{water}\:\mathrm{level}\:\mathrm{rise}\:=\frac{\mathrm{24000}×\:\mathrm{volume}\:\mathrm{of}\:\mathrm{pullet}}{\mathrm{the}\:\mathrm{bottom}\:\mathrm{area}\:\mathrm{of}\:\mathrm{cylinder}} \\ $$$$=\:\frac{\mathrm{24000}×\frac{\mathrm{4}}{\mathrm{3}}\pi×\left(\mathrm{0}.\mathrm{1}\right)^{\mathrm{3}} }{\pi×\mathrm{4}^{\mathrm{2}} }\: \\ $$$$=\:\mathrm{2}\:\mathrm{cm} \\ $$
Commented by tawakalitu last updated on 09/Nov/16
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
