Question Number 136476 by Ar Brandon last updated on 22/Mar/21
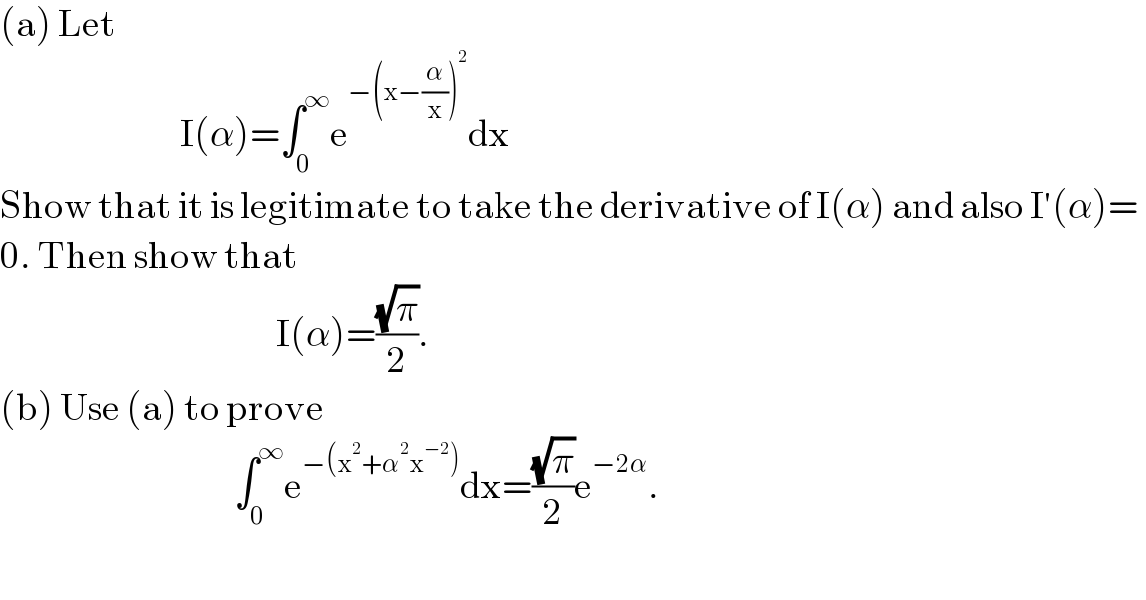
$$\left(\mathrm{a}\right)\:\mathrm{Let}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{x}−\frac{\alpha}{\mathrm{x}}\right)^{\mathrm{2}} } \mathrm{dx} \\ $$$$\mathrm{Show}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{legitimate}\:\mathrm{to}\:\mathrm{take}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{I}\left(\alpha\right)\:\mathrm{and}\:\mathrm{also}\:\mathrm{I}'\left(\alpha\right)= \\ $$$$\mathrm{0}.\:\mathrm{Then}\:\mathrm{show}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\left(\alpha\right)=\frac{\sqrt{\pi}}{\mathrm{2}}. \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Use}\:\left(\mathrm{a}\right)\:\mathrm{to}\:\mathrm{prove} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{x}^{−\mathrm{2}} \right)} \mathrm{dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}\alpha} . \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 22/Mar/21
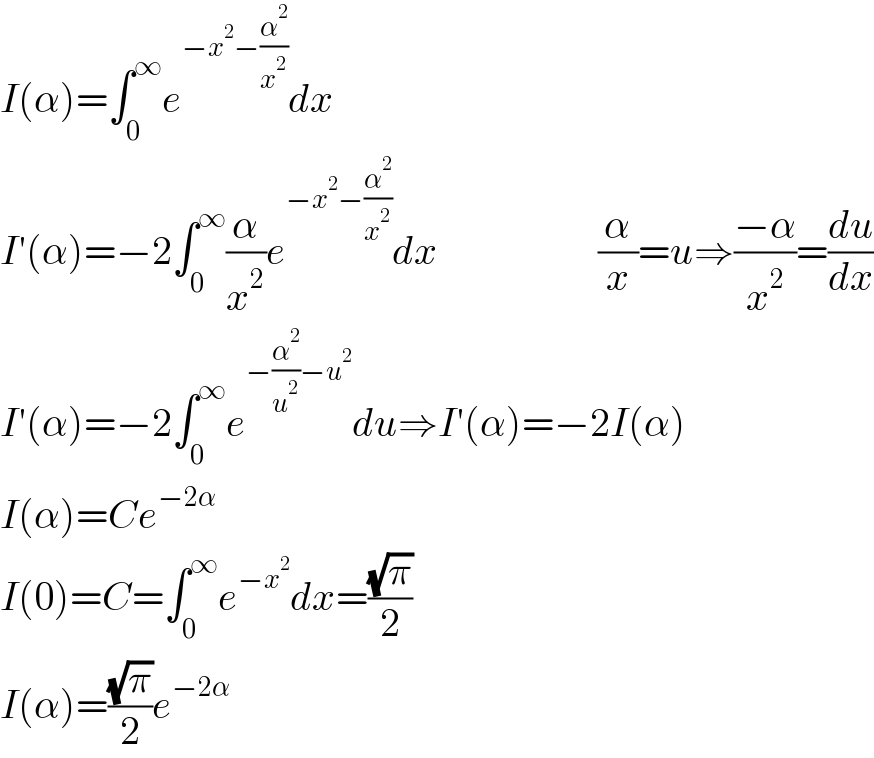
$${I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} −\frac{\alpha^{\mathrm{2}} }{{x}^{\mathrm{2}} }} {dx} \\ $$$${I}'\left(\alpha\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\alpha}{{x}^{\mathrm{2}} }{e}^{−{x}^{\mathrm{2}} −\frac{\alpha^{\mathrm{2}} }{{x}^{\mathrm{2}} }} {dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\alpha}{{x}}={u}\Rightarrow\frac{−\alpha}{{x}^{\mathrm{2}} }=\frac{{du}}{{dx}} \\ $$$${I}'\left(\alpha\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−\frac{\alpha^{\mathrm{2}} }{{u}^{\mathrm{2}} }−{u}^{\mathrm{2}} } {du}\Rightarrow{I}'\left(\alpha\right)=−\mathrm{2}{I}\left(\alpha\right) \\ $$$${I}\left(\alpha\right)={Ce}^{−\mathrm{2}\alpha} \\ $$$${I}\left(\mathrm{0}\right)={C}=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$${I}\left(\alpha\right)=\frac{\sqrt{\pi}}{\mathrm{2}}{e}^{−\mathrm{2}\alpha} \\ $$
