Question Number 72071 by aliesam last updated on 23/Oct/19

$$\left.{a}\right)\underset{{x}\rightarrow\mathrm{0}} {\:{lim}}\frac{\mathrm{3}{x}−{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}{x}−{sin}\left(\mathrm{3}{x}\right)} \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 24/Oct/19
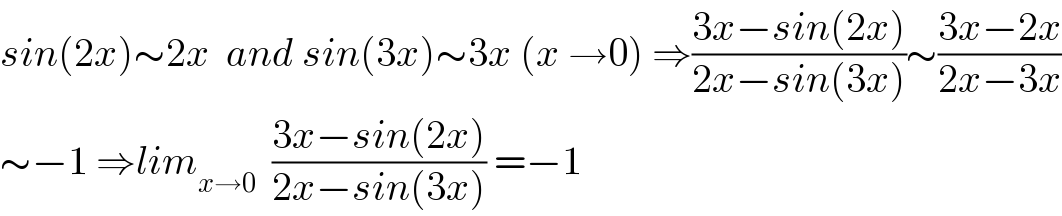
$${sin}\left(\mathrm{2}{x}\right)\sim\mathrm{2}{x}\:\:{and}\:{sin}\left(\mathrm{3}{x}\right)\sim\mathrm{3}{x}\:\left({x}\:\rightarrow\mathrm{0}\right)\:\Rightarrow\frac{\mathrm{3}{x}−{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}{x}−{sin}\left(\mathrm{3}{x}\right)}\sim\frac{\mathrm{3}{x}−\mathrm{2}{x}}{\mathrm{2}{x}−\mathrm{3}{x}} \\ $$$$\sim−\mathrm{1}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{3}{x}−{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}{x}−{sin}\left(\mathrm{3}{x}\right)}\:=−\mathrm{1} \\ $$
Answered by Tanmay chaudhury last updated on 23/Oct/19
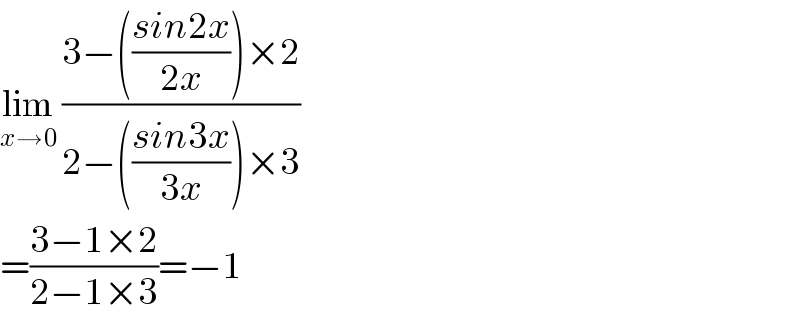
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}−\left(\frac{{sin}\mathrm{2}{x}}{\mathrm{2}{x}}\right)×\mathrm{2}}{\mathrm{2}−\left(\frac{{sin}\mathrm{3}{x}}{\mathrm{3}{x}}\right)×\mathrm{3}} \\ $$$$=\frac{\mathrm{3}−\mathrm{1}×\mathrm{2}}{\mathrm{2}−\mathrm{1}×\mathrm{3}}=−\mathrm{1} \\ $$
Answered by malwaan last updated on 24/Oct/19
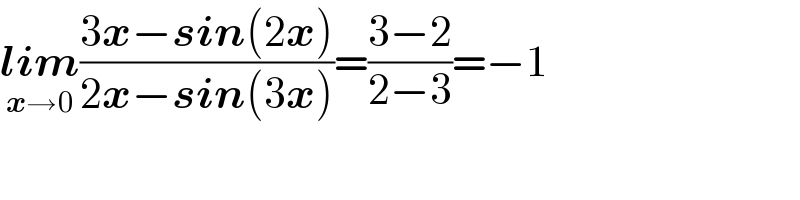
$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\mathrm{3}\boldsymbol{{x}}−\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{x}}\right)}{\mathrm{2}\boldsymbol{{x}}−\boldsymbol{{sin}}\left(\mathrm{3}\boldsymbol{{x}}\right)}=\frac{\mathrm{3}−\mathrm{2}}{\mathrm{2}−\mathrm{3}}=−\mathrm{1} \\ $$
