Menu Close

A-line-passes-through-the-mid-point-of-the-line-joining-the-points-3-4-and-5-6-and-has-a-slope-of-3-4-Find-the-equation-

Tinku Tara
Pin




Question Number 91 by vkulkarni last updated on 25/Jan/15
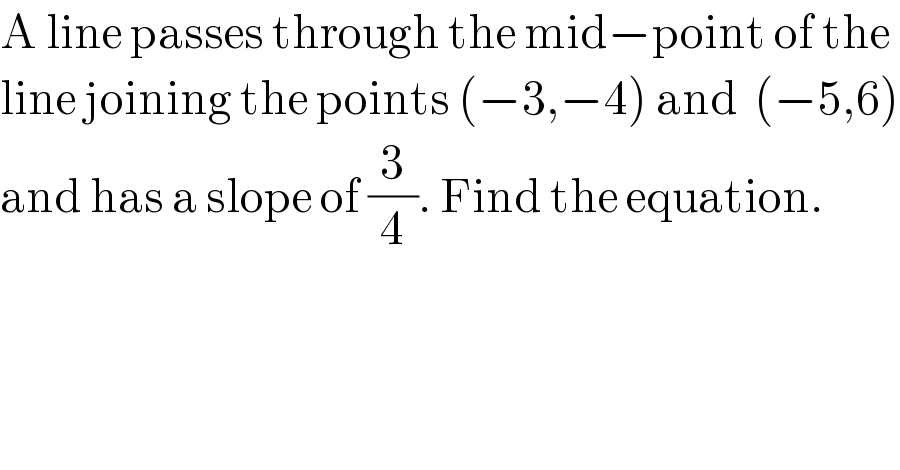
A line passes through the mid−point of the line joining the points (−3,−4) and (−5,6) and has a slope of (3/4). Find the equation.
$$\mathrm{A}\:\mathrm{line}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{mid}−\mathrm{point}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{line}\:\mathrm{joining}\:\mathrm{the}\:\mathrm{points}\:\left(−\mathrm{3},−\mathrm{4}\right)\:\mathrm{and}\:\:\left(−\mathrm{5},\mathrm{6}\right) \\ $$$$\mathrm{and}\:\mathrm{has}\:\mathrm{a}\:\mathrm{slope}\:\mathrm{of}\:\frac{\mathrm{3}}{\mathrm{4}}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}. \\ $$
Answered by ssahoo last updated on 04/Dec/14
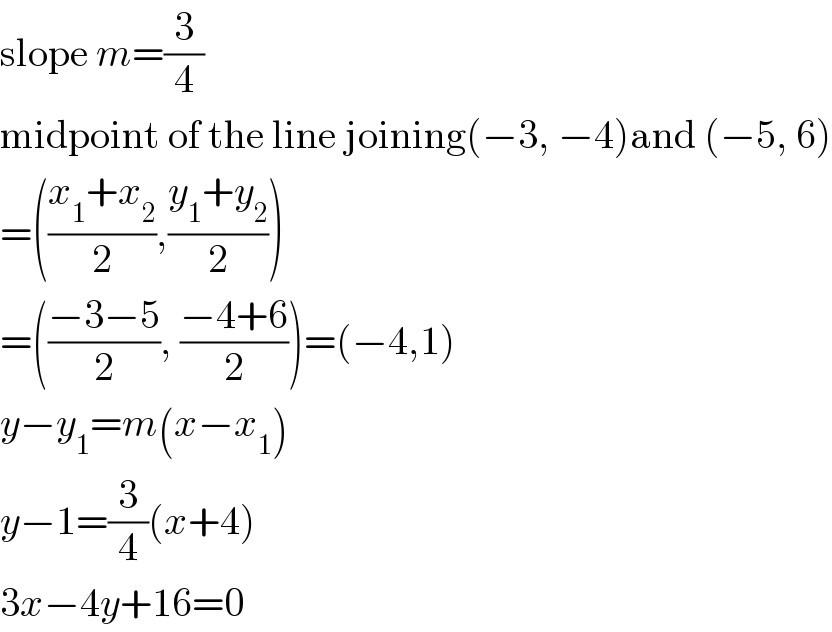
slope m=(3/4) midpoint of the line joining(−3, −4)and (−5, 6) =(((x_1 +x_2 )/2),((y_1 +y_2 )/2)) =(((−3−5)/2), ((−4+6)/2))=(−4,1) y−y_1 =m(x−x_1 ) y−1=(3/4)(x+4) 3x−4y+16=0
$$\mathrm{slope}\:{m}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{midpoint}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{joining}\left(−\mathrm{3},\:−\mathrm{4}\right)\mathrm{and}\:\left(−\mathrm{5},\:\mathrm{6}\right) \\ $$$$=\left(\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}},\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} }{\mathrm{2}}\right)\: \\ $$$$=\left(\frac{−\mathrm{3}−\mathrm{5}}{\mathrm{2}},\:\frac{−\mathrm{4}+\mathrm{6}}{\mathrm{2}}\right)=\left(−\mathrm{4},\mathrm{1}\right) \\ $$$${y}−{y}_{\mathrm{1}} ={m}\left({x}−{x}_{\mathrm{1}} \right) \\ $$$${y}−\mathrm{1}=\frac{\mathrm{3}}{\mathrm{4}}\left({x}+\mathrm{4}\right) \\ $$$$\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{16}=\mathrm{0} \\ $$

Pin