Question Number 10069 by Tawakalitu ayo mi last updated on 23/Jan/17

$$\mathrm{A}\:\mathrm{man}\:\mathrm{can}\:\mathrm{row}\:\mathrm{a}\:\mathrm{boat}\:\mathrm{at}\:\mathrm{4}\:\mathrm{km}/\mathrm{hr}\:\mathrm{in}\:\mathrm{still}\:\mathrm{water}. \\ $$$$\mathrm{He}\:\mathrm{row}\:\mathrm{the}\:\mathrm{boat}\:\mathrm{2km}\:\mathrm{upstream}\:\mathrm{and}\:\mathrm{2km}\:\mathrm{back} \\ $$$$\mathrm{to}\:\mathrm{his}\:\mathrm{starting}\:\mathrm{place}\:\mathrm{in}\:\mathrm{2}\:\mathrm{hours}.\:\mathrm{How}\:\mathrm{fast}\:\mathrm{is}\: \\ $$$$\mathrm{the}\:\mathrm{stream}\:\mathrm{flowing}. \\ $$
Commented by ridwan balatif last updated on 23/Jan/17

Commented by Tawakalitu ayo mi last updated on 23/Jan/17
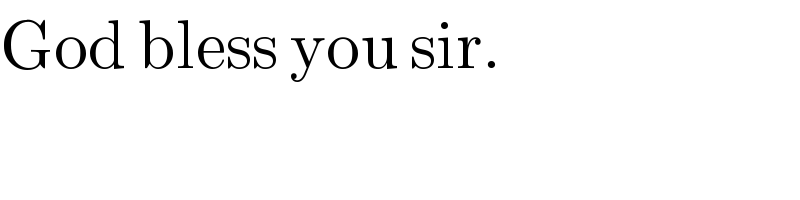
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 23/Jan/17

$$\mathrm{let}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{the}\:\mathrm{stream}=\mathrm{x}\:\mathrm{km}/\mathrm{h} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{upstream}\:=\left(\mathrm{4}+\mathrm{x}\right)\:\mathrm{km}/\mathrm{h} \\ $$$$\mathrm{the}\:\mathrm{velocity}\:\mathrm{when}\:\mathrm{he}\:\mathrm{rows}\:\mathrm{back}=\left(\mathrm{4}−\mathrm{x}\right)\:\mathrm{km}/\mathrm{h} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\Rightarrow\:\frac{\mathrm{2}}{\mathrm{4}+\mathrm{x}}\:+\:\frac{\mathrm{2}}{\mathrm{4}−\mathrm{x}}\:=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\left(\mathrm{4}−\mathrm{x}\right)+\mathrm{2}\left(\mathrm{4}+\mathrm{x}\right)}{\left(\mathrm{4}+\mathrm{x}\right)\left(\mathrm{4}−\mathrm{x}\right)}\:=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{8}−\mathrm{2x}+\mathrm{8}+\mathrm{2x}}{\mathrm{16}−\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{16}−\mathrm{x}^{\mathrm{2}} =\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{8}\:\Rightarrow\:\mathrm{x}=\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{km}/\mathrm{h} \\ $$
Commented by Tawakalitu ayo mi last updated on 23/Jan/17
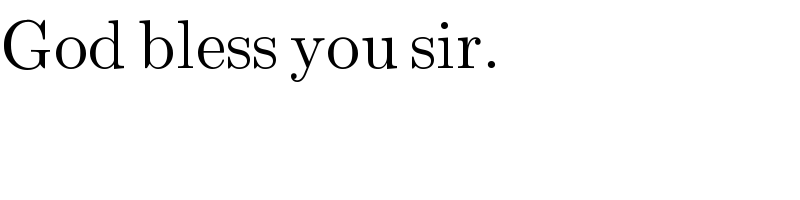
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
