Question Number 12699 by chux last updated on 29/Apr/17

$$\mathrm{A}\:\mathrm{man}\:\mathrm{can}\:\mathrm{row}\:\mathrm{a}\:\mathrm{boat}\:\mathrm{at}\:\mathrm{4km}/\mathrm{hr} \\ $$$$\mathrm{in}\:\mathrm{still}\:\mathrm{water}.\mathrm{He}\:\mathrm{rows}\:\mathrm{the}\:\mathrm{boat}\:\mathrm{2km} \\ $$$$\mathrm{upstream}\:\mathrm{and}\:\mathrm{2km}\:\mathrm{back}\:\mathrm{to}\:\mathrm{his} \\ $$$$\mathrm{starting}\:\mathrm{place}\:\mathrm{in}\:\mathrm{2hours}.\mathrm{How}\:\mathrm{fast} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{stream}\:\mathrm{moving}? \\ $$$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help} \\ $$
Answered by mrW1 last updated on 29/Apr/17
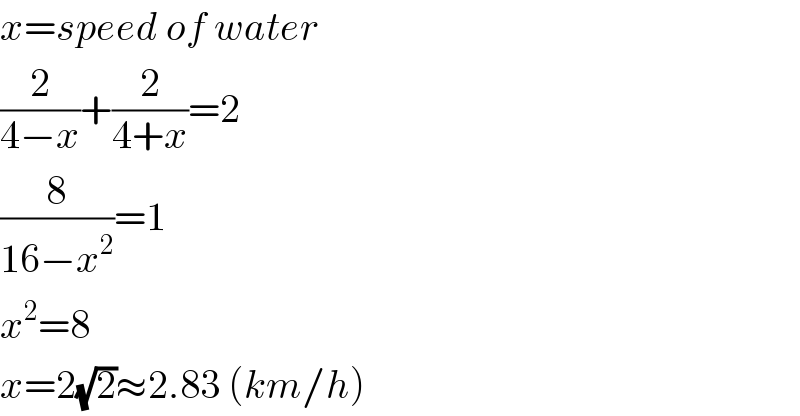
$${x}={speed}\:{of}\:{water} \\ $$$$\frac{\mathrm{2}}{\mathrm{4}−{x}}+\frac{\mathrm{2}}{\mathrm{4}+{x}}=\mathrm{2} \\ $$$$\frac{\mathrm{8}}{\mathrm{16}−{x}^{\mathrm{2}} }=\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\mathrm{8} \\ $$$${x}=\mathrm{2}\sqrt{\mathrm{2}}\approx\mathrm{2}.\mathrm{83}\:\left({km}/{h}\right) \\ $$
Commented by chux last updated on 29/Apr/17

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{pls}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{concept} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{and}\:\mathrm{lower} \\ $$$$\mathrm{stream}. \\ $$
Commented by mrW1 last updated on 30/Apr/17

$${when}\:{the}\:{man}\:{rows}\:{against}\:{the}\:{stream}, \\ $$$${if}\:{the}\:{water}\:{were}\:{still},\:{the}\:{could}\:{row} \\ $$$$\mathrm{4}\:{km}\:{in}\:{one}\:{hour}.\:{in}\:{this}\:{one}\:{hour}\:{the} \\ $$$${water}\:{brings}\:{ihm}\:{x}\:{km}\:{back},\:{i}.{e}.\:{his} \\ $$$${speed}\:{relatively}\:{to}\:{the}\:{coast}\:{is}\:\left(\mathrm{4}−{x}\right)\:{km}/{hr}. \\ $$$${when}\:{he}\:{rows}\:{in}\:{the}\:{direction}\:{of}\:{the} \\ $$$${steam},\:{his}\:{speed}\:{relatively}\:{to}\:{the} \\ $$$${coast}\:{is}\:\left(\mathrm{4}+{x}\right)\:{km}/{hr}.\:{since}\:{he}\:{rows} \\ $$$$\mathrm{2}\:{km}\:{upper}\:{steam}\:{and}\:\mathrm{2}\:{km}\:{back}\:{in} \\ $$$${totally}\:\mathrm{2}\:{hours},\:{we}\:{have} \\ $$$$\frac{\mathrm{2}}{\mathrm{4}−{x}}+\frac{\mathrm{2}}{\mathrm{4}+{x}}=\mathrm{2} \\ $$
Commented by chux last updated on 30/Apr/17
$$\mathrm{thanks}\:….\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{this}. \\ $$
