Question Number 139232 by Dwaipayan Shikari last updated on 24/Apr/21

$${A}\:{man}\:{has}\:'{n}'\:{pair}\:{of}\:{black}\:{shoes}\:{and}\:'{m}' \\ $$$${pairs}\:{of}\:{brown}\:{shoes}.\:{Man}\:{hurriedly}\:{wear} \\ $$$${two}\:{shoes}.\:{What}\:{is}\:{probability}\:{that}\:{both}\:{of} \\ $$$${them}\:{are}\:{black}? \\ $$
Commented by mr W last updated on 24/Apr/21

$${when}\:{he}\:{has}\:{only}\:{black}\:{shoes},\:{is}\:{it}\:{not} \\ $$$$\mathrm{100\%}? \\ $$
Commented by yuXfar last updated on 24/Apr/21
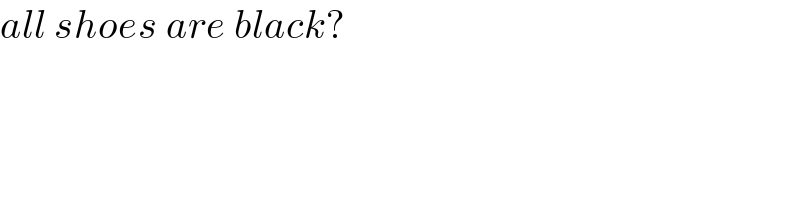
$${all}\:{shoes}\:{are}\:{black}? \\ $$
Commented by Dwaipayan Shikari last updated on 24/Apr/21
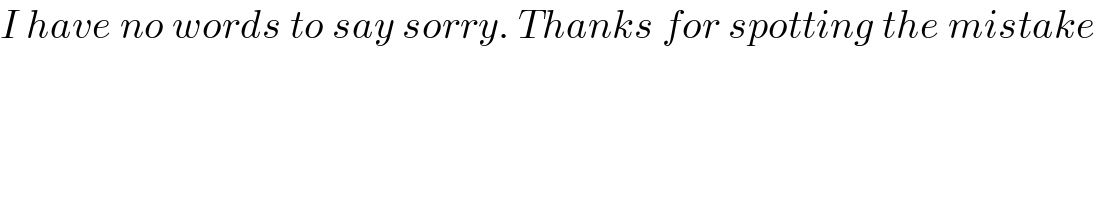
$${I}\:{have}\:{no}\:{words}\:{to}\:{say}\:{sorry}.\:{Thanks}\:{for}\:{spotting}\:{the}\:{mistake} \\ $$
Commented by mr W last updated on 24/Apr/21
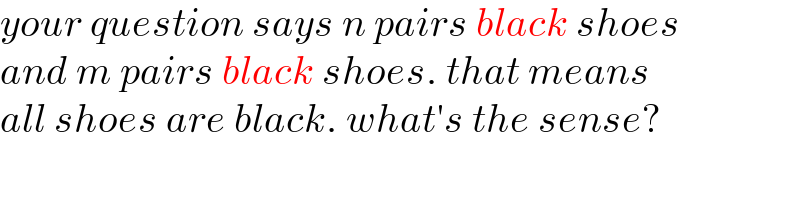
$${your}\:{question}\:{says}\:{n}\:{pairs}\:{black}\:{shoes} \\ $$$${and}\:{m}\:{pairs}\:{black}\:{shoes}.\:{that}\:{means} \\ $$$${all}\:{shoes}\:{are}\:{black}.\:{what}'{s}\:{the}\:{sense}? \\ $$
Answered by yuXfar last updated on 24/Apr/21

$${considering}\:{that}\:{shoes}\:{are}\:{chosen}\: \\ $$$${as}\:{pairs}\:{and}\:{not}\:{individually} \\ $$$$\left(\frac{{n}}{{n}+{m}}\right) \\ $$
