Menu Close

a-n-1-2-3-4-5-n-n-1-mod-2-a-n-1-2-3-4-5-6-n-n-0-mod-2-lim-n-a-n-1-

Tinku Tara
Pin




Question Number 348 by 123456 last updated on 23/Dec/14
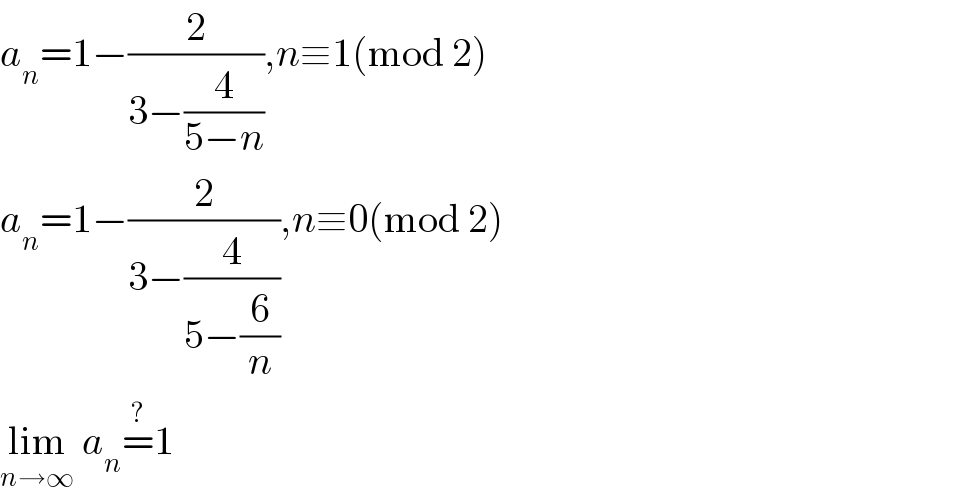
a_n =1−(2/(3−(4/(5−n)))),n≡1(mod 2) a_n =1−(2/(3−(4/(5−(6/n))))),n≡0(mod 2) lim_(n→∞) a_n =^? 1
$${a}_{{n}} =\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{4}}{\mathrm{5}−{n}}},{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$${a}_{{n}} =\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{4}}{\mathrm{5}−\frac{\mathrm{6}}{{n}}}},{n}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \overset{?} {=}\mathrm{1} \\ $$
Commented by 123456 last updated on 23/Dec/14
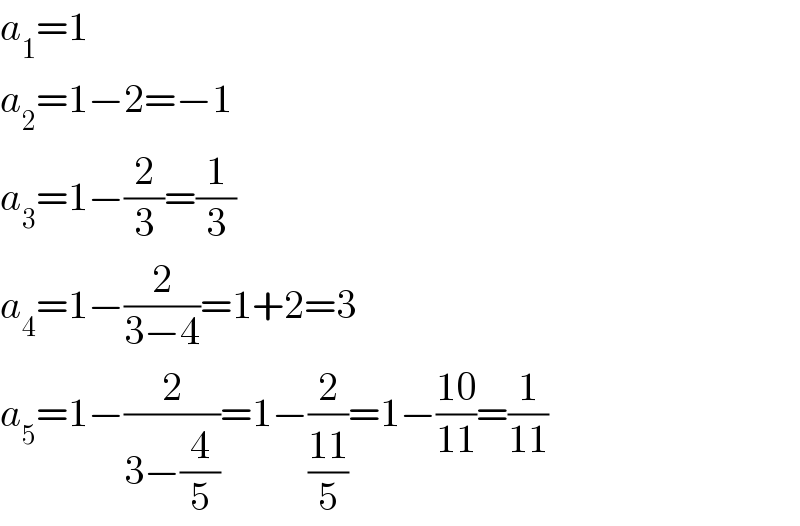
a_1 =1 a_2 =1−2=−1 a_3 =1−(2/3)=(1/3) a_4 =1−(2/(3−4))=1+2=3 a_5 =1−(2/(3−(4/5)))=1−(2/((11)/5))=1−((10)/(11))=(1/(11))
$${a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1} \\ $$$${a}_{\mathrm{3}} =\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${a}_{\mathrm{4}} =\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}−\mathrm{4}}=\mathrm{1}+\mathrm{2}=\mathrm{3} \\ $$$${a}_{\mathrm{5}} =\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{4}}{\mathrm{5}}}=\mathrm{1}−\frac{\mathrm{2}}{\frac{\mathrm{11}}{\mathrm{5}}}=\mathrm{1}−\frac{\mathrm{10}}{\mathrm{11}}=\frac{\mathrm{1}}{\mathrm{11}} \\ $$

Pin