Question Number 2329 by 123456 last updated on 16/Nov/15
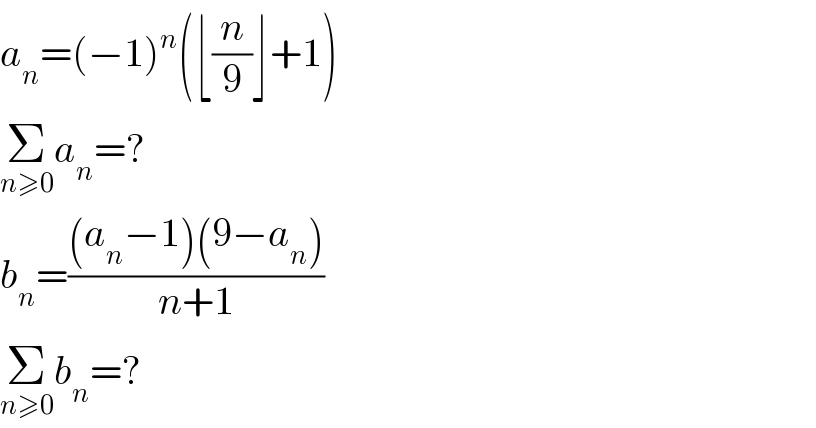
$${a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left(\lfloor\frac{{n}}{\mathrm{9}}\rfloor+\mathrm{1}\right) \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{a}_{{n}} =? \\ $$$${b}_{{n}} =\frac{\left({a}_{{n}} −\mathrm{1}\right)\left(\mathrm{9}−{a}_{{n}} \right)}{{n}+\mathrm{1}} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{b}_{{n}} =? \\ $$
Commented by prakash jain last updated on 16/Nov/15
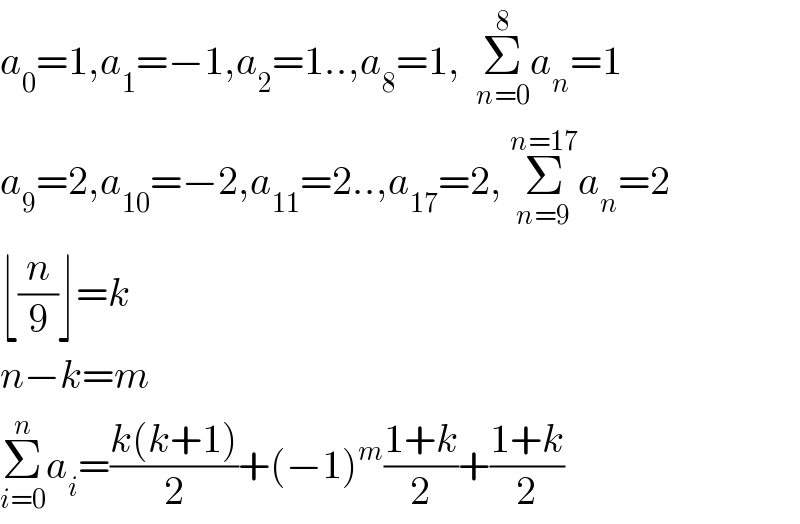
$${a}_{\mathrm{0}} =\mathrm{1},{a}_{\mathrm{1}} =−\mathrm{1},{a}_{\mathrm{2}} =\mathrm{1}..,{a}_{\mathrm{8}} =\mathrm{1},\:\:\underset{{n}=\mathrm{0}} {\overset{\mathrm{8}} {\sum}}{a}_{{n}} =\mathrm{1} \\ $$$${a}_{\mathrm{9}} =\mathrm{2},{a}_{\mathrm{10}} =−\mathrm{2},{a}_{\mathrm{11}} =\mathrm{2}..,{a}_{\mathrm{17}} =\mathrm{2},\:\underset{{n}=\mathrm{9}} {\overset{{n}=\mathrm{17}} {\sum}}{a}_{{n}} =\mathrm{2} \\ $$$$\lfloor\frac{{n}}{\mathrm{9}}\rfloor={k} \\ $$$${n}−{k}={m} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} =\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}+\left(−\mathrm{1}\right)^{{m}} \frac{\mathrm{1}+{k}}{\mathrm{2}}+\frac{\mathrm{1}+{k}}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 16/Nov/15
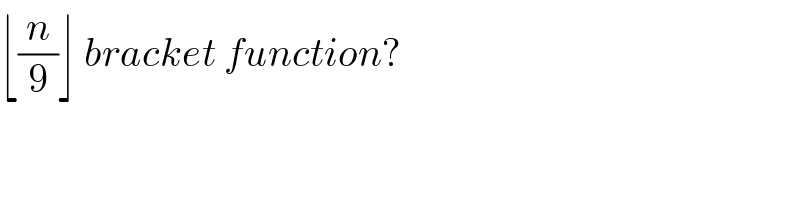
$$\lfloor\frac{{n}}{\mathrm{9}}\rfloor\:{bracket}\:{function}? \\ $$
Commented by 123456 last updated on 16/Nov/15
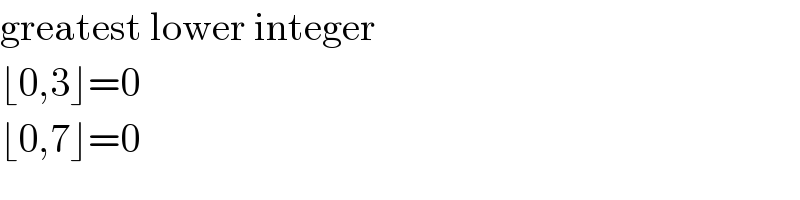
$$\mathrm{greatest}\:\mathrm{lower}\:\mathrm{integer} \\ $$$$\lfloor\mathrm{0},\mathrm{3}\rfloor=\mathrm{0} \\ $$$$\lfloor\mathrm{0},\mathrm{7}\rfloor=\mathrm{0} \\ $$
