Question Number 12946 by 433 last updated on 07/May/17
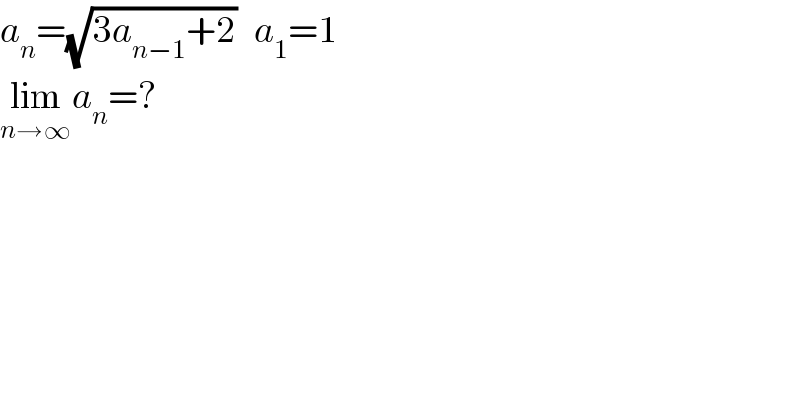
$${a}_{{n}} =\sqrt{\mathrm{3}{a}_{{n}−\mathrm{1}} +\mathrm{2}}\:\:\:{a}_{\mathrm{1}} =\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =? \\ $$
Answered by ajfour last updated on 07/May/17
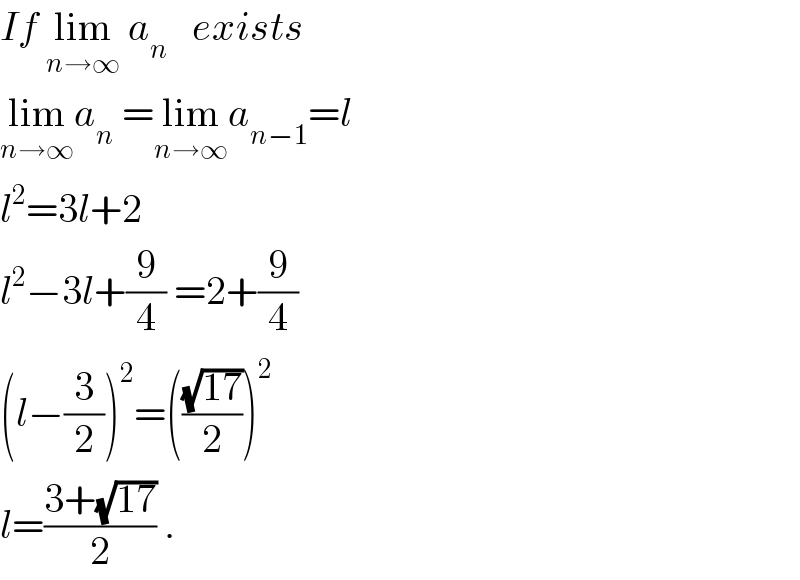
$${If}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:\:\:{exists} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} \:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}−\mathrm{1}} ={l} \\ $$$${l}^{\mathrm{2}} =\mathrm{3}{l}+\mathrm{2} \\ $$$${l}^{\mathrm{2}} −\mathrm{3}{l}+\frac{\mathrm{9}}{\mathrm{4}}\:=\mathrm{2}+\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\left({l}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${l}=\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}\:. \\ $$
