Question Number 4597 by FilupSmith last updated on 10/Feb/16

$${a}_{{n}} =\sqrt{{a}_{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} ={c} \\ $$$$ \\ $$$$\mathrm{Solve}: \\ $$$${S}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \\ $$
Commented by FilupSmith last updated on 10/Feb/16
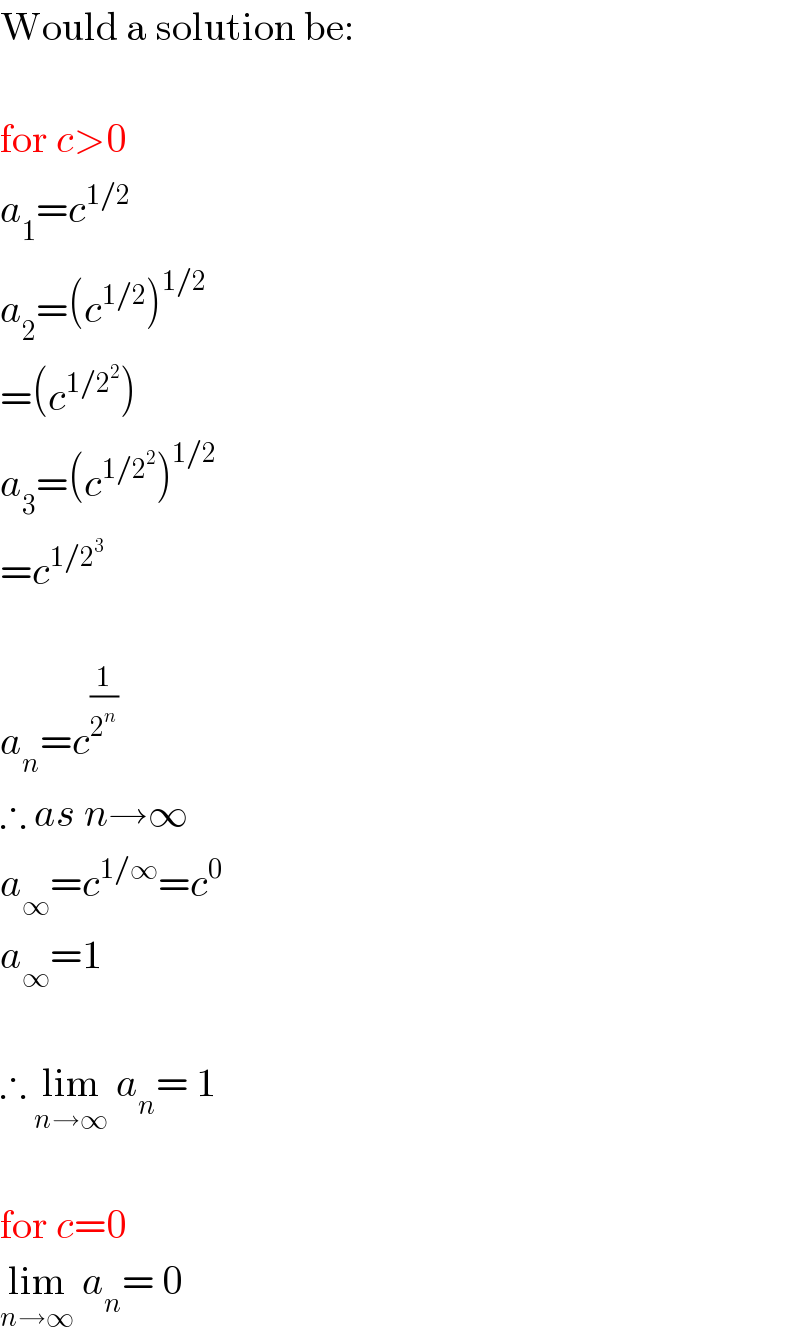
$$\mathrm{Would}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{be}: \\ $$$$ \\ $$$$\mathrm{for}\:{c}>\mathrm{0} \\ $$$${a}_{\mathrm{1}} ={c}^{\mathrm{1}/\mathrm{2}} \\ $$$${a}_{\mathrm{2}} =\left({c}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\left({c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \right) \\ $$$${a}_{\mathrm{3}} =\left({c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{3}} } \\ $$$$ \\ $$$${a}_{{n}} ={c}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} \\ $$$$\therefore\:{as}\:{n}\rightarrow\infty \\ $$$${a}_{\infty} ={c}^{\mathrm{1}/\infty} ={c}^{\mathrm{0}} \\ $$$${a}_{\infty} =\mathrm{1} \\ $$$$ \\ $$$$\therefore\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\:\mathrm{1} \\ $$$$ \\ $$$$\mathrm{for}\:{c}=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\:\mathrm{0} \\ $$
Commented by Yozzii last updated on 10/Feb/16

$${This}\:{appears}\:{to}\:{be}\:{legitimate}\:{for}\:{if} \\ $$$${c}=\mathrm{0},\:{a}_{{n}} =\mathrm{0}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } =\mathrm{0}\:\:\forall{n}\in\mathbb{N}\Rightarrow\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{a}_{{n}} =\underset{{n}\rightarrow+\infty} {\mathrm{lim}0}=\mathrm{0}. \\ $$$${The}\:{term}\:{a}_{\infty} \:{does}\:{not}\:{exist}\:{by}\:{the}\:{way}. \\ $$$${It}'{s}\:{better}\:{to}\:{say}\:'\:{as}\:{n}\rightarrow\infty,\:\mathrm{2}^{{n}−\mathrm{1}} \rightarrow\infty \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\rightarrow\mathrm{0}\Rightarrow{c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } \rightarrow{c}^{\mathrm{0}} =\mathrm{1}\Rightarrow{a}_{{n}} \rightarrow\mathrm{1}.' \\ $$$${To}\:{further}\:{convince}\:{your}\:{audience} \\ $$$${of}\:{the}\:{obvious}\:{pattern}\:{that}\:{a}_{{n}} ={c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } , \\ $$$${given}\:{that}\:{a}_{\mathrm{1}} ={c}>\mathrm{0}\:{and}\:{a}_{{n}+\mathrm{1}} =\sqrt{{a}_{{n}} }, \\ $$$${use}\:{induction}\:{on}\:{n}.\:\left({I}\:{saw}\:{that}\:{you}\right. \\ $$$${wrote}\:{a}_{\mathrm{1}} ={c}^{\mathrm{1}/\mathrm{2}} \:{when}\:{the}\:{information} \\ $$$${gave}\:{a}_{\mathrm{1}} ={c}.\:{It}'{s}\:{really}\:{a}_{\mathrm{2}} =\sqrt{{a}_{\mathrm{1}} }={c}^{\mathrm{1}/\mathrm{2}} \Rightarrow \\ $$$$\left.{a}_{\mathrm{3}} =\sqrt{{a}_{\mathrm{2}} }={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \Rightarrow{a}_{\mathrm{4}} =\sqrt{{a}_{\mathrm{3}} }={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{3}} } \Rightarrow…\Rightarrow{a}_{{n}} ={c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } \:\:\left({n}\in\mathbb{N}\right).\right) \\ $$$$ \\ $$
Commented by FilupSmith last updated on 11/Feb/16

$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{know}\:\mathrm{induction}.\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{been}\:\mathrm{meaning}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{but}\:\mathrm{i}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{find}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{explanation} \\ $$
Commented by Yozzii last updated on 11/Feb/16

$${The}\:{underlying}\:{principle}\:{of}\: \\ $$$${mathematical}\:{induction}\:{is}\: \\ $$$${the}\:{idea}\:{that}\:{you}\:{can}\:{obtain}\:{an}\:{integer} \\ $$$${k}+\mathrm{1}\:{if}\:{you}\:{know}\:{what}\:{k}\:{is},{being}\:{an} \\ $$$${integer}.\:{So},\:{given}\:{an}\:{integer}\:{k}\: \\ $$$${you}\:{can}\:{get}\:{the}\:{next}\:{integer}\:{by}\:{adding} \\ $$$$\mathrm{1}\:{to}\:{k}\Rightarrow{k}+\mathrm{1}.\:{So},\:{since}\:{you}\:{know}\: \\ $$$${what}\:{your}\:{initial}\:{integer}\:{is},\:{e}.{g}\:\mathrm{1}, \\ $$$${you}\:{can}\:{find}\:{any}\:{integer}\:{greater}\:{than} \\ $$$$\left({or}\:{less}\:{than}\right)\:\mathrm{1}\:{if}\:{you}\:{continue}\:{on} \\ $$$${from}\:\mathrm{1}\:{to}\:\mathrm{2}\:,{then}\:\mathrm{2}\:{to}\:\mathrm{3}\:,{then}\:\mathrm{3}\:{to}\:\mathrm{4}, \\ $$$$….,\:{then}\:{k}\:{to}\:{k}+\mathrm{1},{then}….{to}\:{infinity}. \\ $$$${You}\:{can}\:{assign}\:{a}\:{mathematical} \\ $$$${idea}\:{P}\:\:{that}\:{depends}\:{on}\:{n}\:{to}\:{use}\: \\ $$$${induction}\:{to}\:{show}\:{that}\:{P}\left({n}\right)\:{is}\:{true} \\ $$$${for}\:{all}\:{integers}\:{n}\:{since}\:{from},\:{say}\:{P}\left(\mathrm{1}\right), \\ $$$${you}\:{can}\:{deduce}\:{P}\left({k}\right),{P}\left({k}+\mathrm{1}\right),{P}\left({k}+\mathrm{2}\right)…. \\ $$$$ \\ $$$$ \\ $$
