Menu Close

a-n-m-m-n-0-a-n-1-m-2-n-gt-0-n-0-mod-2-a-n-2-m-1-nn-n-gt-0-n-1-mod-2-m-0-a-m-1-n-1-a-n-2-m-2-n-gt-0-n-1-mod-2-m-gt-0-evaluate-a-7-5-

Tinku Tara
Pin




Question Number 291 by 123456 last updated on 25/Jan/15
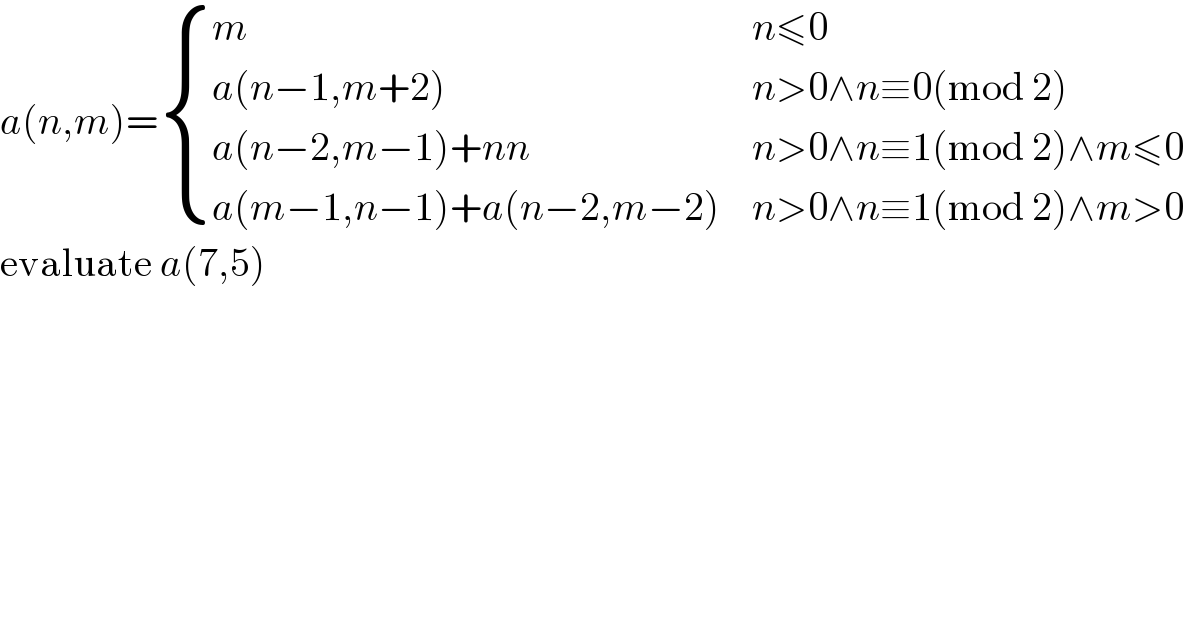
a(n,m)= { (m,(n≤0)),((a(n−1,m+2)),(n>0∧n≡0(mod 2))),((a(n−2,m−1)+nn),(n>0∧n≡1(mod 2)∧m≤0)),((a(m−1,n−1)+a(n−2,m−2)),(n>0∧n≡1(mod 2)∧m>0)) :} evaluate a(7,5)
$${a}\left({n},{m}\right)=\begin{cases}{{m}}&{{n}\leqslant\mathrm{0}}\\{{a}\left({n}−\mathrm{1},{m}+\mathrm{2}\right)}&{{n}>\mathrm{0}\wedge{n}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right)}\\{{a}\left({n}−\mathrm{2},{m}−\mathrm{1}\right)+{nn}}&{{n}>\mathrm{0}\wedge{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right)\wedge{m}\leqslant\mathrm{0}}\\{{a}\left({m}−\mathrm{1},{n}−\mathrm{1}\right)+{a}\left({n}−\mathrm{2},{m}−\mathrm{2}\right)}&{{n}>\mathrm{0}\wedge{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right)\wedge{m}>\mathrm{0}}\end{cases} \\ $$$$\mathrm{evaluate}\:{a}\left(\mathrm{7},\mathrm{5}\right) \\ $$
Answered by prakash jain last updated on 19/Dec/14
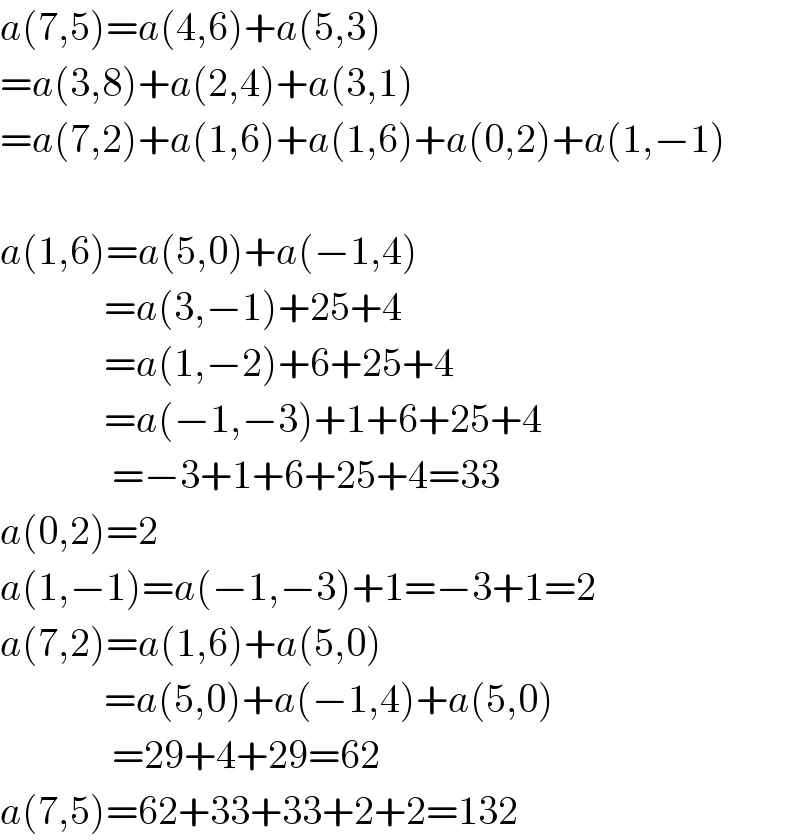
a(7,5)=a(4,6)+a(5,3) =a(3,8)+a(2,4)+a(3,1) =a(7,2)+a(1,6)+a(1,6)+a(0,2)+a(1,−1) a(1,6)=a(5,0)+a(−1,4) =a(3,−1)+25+4 =a(1,−2)+6+25+4 =a(−1,−3)+1+6+25+4 =−3+1+6+25+4=33 a(0,2)=2 a(1,−1)=a(−1,−3)+1=−3+1=2 a(7,2)=a(1,6)+a(5,0) =a(5,0)+a(−1,4)+a(5,0) =29+4+29=62 a(7,5)=62+33+33+2+2=132
$${a}\left(\mathrm{7},\mathrm{5}\right)={a}\left(\mathrm{4},\mathrm{6}\right)+{a}\left(\mathrm{5},\mathrm{3}\right) \\ $$$$={a}\left(\mathrm{3},\mathrm{8}\right)+{a}\left(\mathrm{2},\mathrm{4}\right)+{a}\left(\mathrm{3},\mathrm{1}\right) \\ $$$$={a}\left(\mathrm{7},\mathrm{2}\right)+{a}\left(\mathrm{1},\mathrm{6}\right)+{a}\left(\mathrm{1},\mathrm{6}\right)+{a}\left(\mathrm{0},\mathrm{2}\right)+{a}\left(\mathrm{1},−\mathrm{1}\right) \\ $$$$ \\ $$$${a}\left(\mathrm{1},\mathrm{6}\right)={a}\left(\mathrm{5},\mathrm{0}\right)+{a}\left(−\mathrm{1},\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={a}\left(\mathrm{3},−\mathrm{1}\right)+\mathrm{25}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={a}\left(\mathrm{1},−\mathrm{2}\right)+\mathrm{6}+\mathrm{25}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={a}\left(−\mathrm{1},−\mathrm{3}\right)+\mathrm{1}+\mathrm{6}+\mathrm{25}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{3}+\mathrm{1}+\mathrm{6}+\mathrm{25}+\mathrm{4}=\mathrm{33} \\ $$$${a}\left(\mathrm{0},\mathrm{2}\right)=\mathrm{2} \\ $$$${a}\left(\mathrm{1},−\mathrm{1}\right)={a}\left(−\mathrm{1},−\mathrm{3}\right)+\mathrm{1}=−\mathrm{3}+\mathrm{1}=\mathrm{2} \\ $$$${a}\left(\mathrm{7},\mathrm{2}\right)={a}\left(\mathrm{1},\mathrm{6}\right)+{a}\left(\mathrm{5},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={a}\left(\mathrm{5},\mathrm{0}\right)+{a}\left(−\mathrm{1},\mathrm{4}\right)+{a}\left(\mathrm{5},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{29}+\mathrm{4}+\mathrm{29}=\mathrm{62} \\ $$$${a}\left(\mathrm{7},\mathrm{5}\right)=\mathrm{62}+\mathrm{33}+\mathrm{33}+\mathrm{2}+\mathrm{2}=\mathrm{132} \\ $$

Pin