Menu Close

A-parabola-with-equation-y-x-2-k-5-intersects-a-circle-with-equation-x-2-y-2-25-at-exactly-3-points-A-B-C-Determine-all-such-positive-integers-k-for-which-the-area-of-ABC-is-an-integer

Tinku Tara 0 Comments
Pin




Question Number 11607 by Joel576 last updated on 29/Mar/17
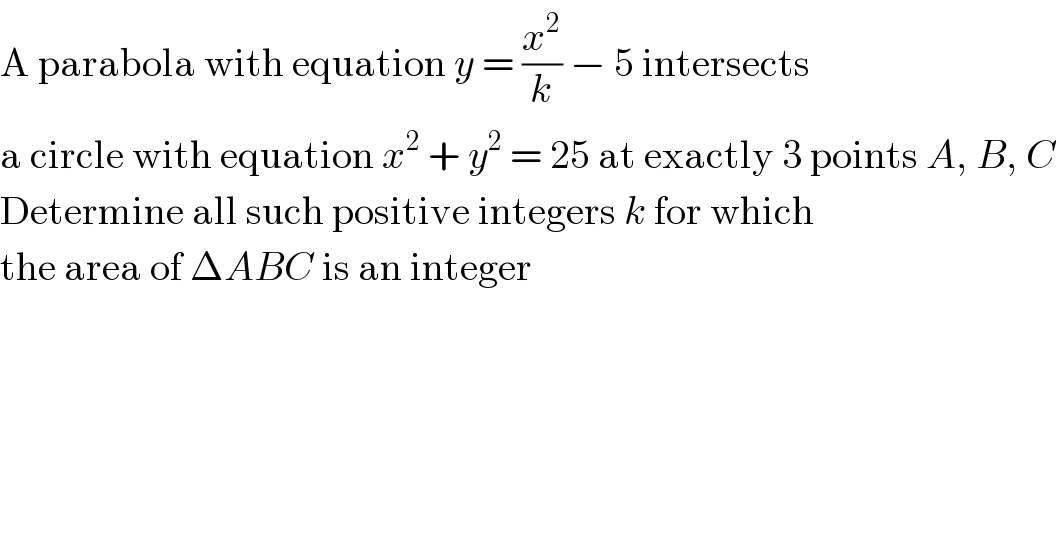
A parabola with equation y = (x^2 /k) − 5 intersects a circle with equation x^2 + y^2 = 25 at exactly 3 points A, B, C Determine all such positive integers k for which the area of ΔABC is an integer
$$\mathrm{A}\:\mathrm{parabola}\:\mathrm{with}\:\mathrm{equation}\:{y}\:=\:\frac{{x}^{\mathrm{2}} }{{k}}\:−\:\mathrm{5}\:\mathrm{intersects} \\ $$$$\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{equation}\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:=\:\mathrm{25}\:\mathrm{at}\:\mathrm{exactly}\:\mathrm{3}\:\mathrm{points}\:{A},\:{B},\:{C} \\ $$$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{such}\:\mathrm{positive}\:\mathrm{integers}\:{k}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\Delta{ABC}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer} \\ $$
Answered by mrW1 last updated on 29/Mar/17
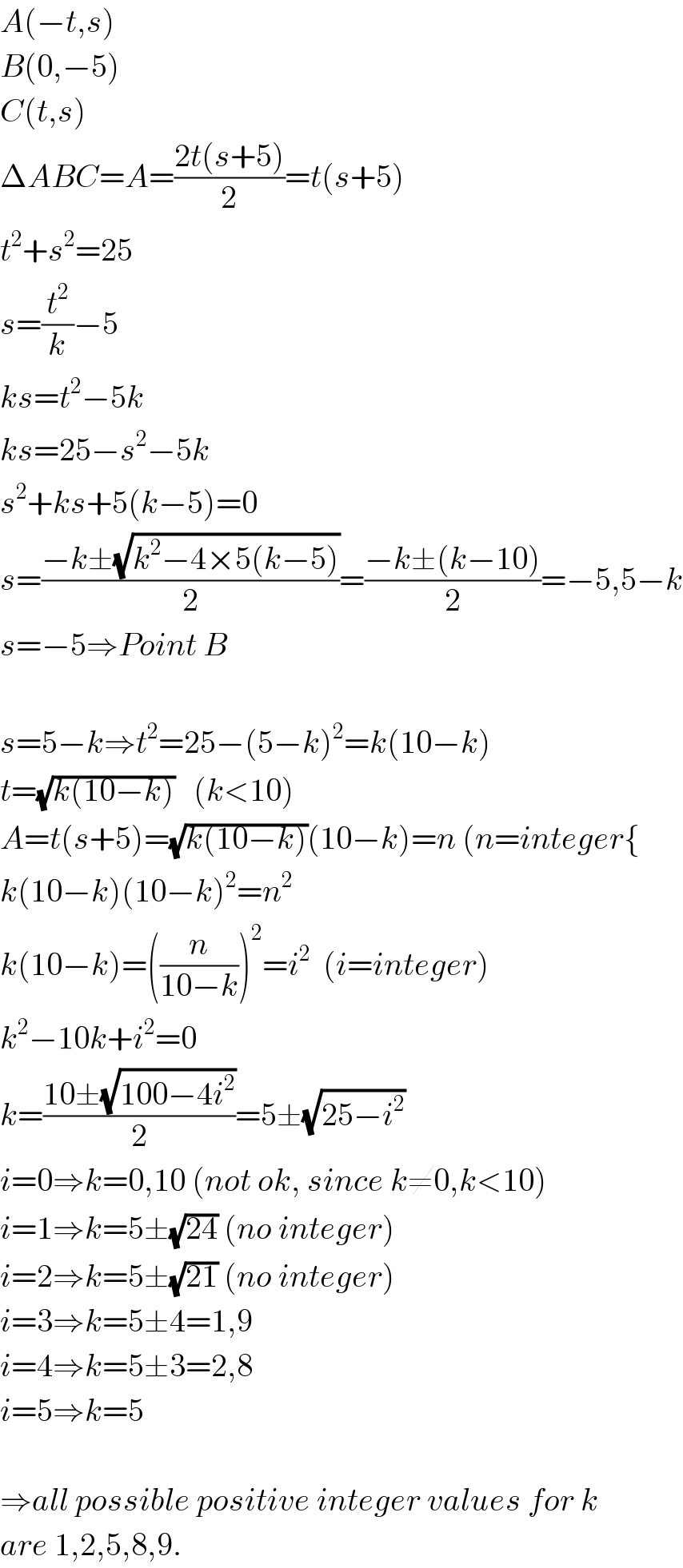
A(−t,s) B(0,−5) C(t,s) ΔABC=A=((2t(s+5))/2)=t(s+5) t^2 +s^2 =25 s=(t^2 /k)−5 ks=t^2 −5k ks=25−s^2 −5k s^2 +ks+5(k−5)=0 s=((−k±(√(k^2 −4×5(k−5))))/2)=((−k±(k−10))/2)=−5,5−k s=−5⇒Point B s=5−k⇒t^2 =25−(5−k)^2 =k(10−k) t=(√(k(10−k))) (k<10) A=t(s+5)=(√(k(10−k)))(10−k)=n (n=integer{ k(10−k)(10−k)^2 =n^2 k(10−k)=((n/(10−k)))^2 =i^2 (i=integer) k^2 −10k+i^2 =0 k=((10±(√(100−4i^2 )))/2)=5±(√(25−i^2 )) i=0⇒k=0,10 (not ok, since k≠0,k<10) i=1⇒k=5±(√(24)) (no integer) i=2⇒k=5±(√(21)) (no integer) i=3⇒k=5±4=1,9 i=4⇒k=5±3=2,8 i=5⇒k=5 ⇒all possible positive integer values for k are 1,2,5,8,9.
$${A}\left(−{t},{s}\right) \\ $$$${B}\left(\mathrm{0},−\mathrm{5}\right) \\ $$$${C}\left({t},{s}\right) \\ $$$$\Delta{ABC}={A}=\frac{\mathrm{2}{t}\left({s}+\mathrm{5}\right)}{\mathrm{2}}={t}\left({s}+\mathrm{5}\right) \\ $$$${t}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{25} \\ $$$${s}=\frac{{t}^{\mathrm{2}} }{{k}}−\mathrm{5} \\ $$$${ks}={t}^{\mathrm{2}} −\mathrm{5}{k} \\ $$$${ks}=\mathrm{25}−{s}^{\mathrm{2}} −\mathrm{5}{k} \\ $$$${s}^{\mathrm{2}} +{ks}+\mathrm{5}\left({k}−\mathrm{5}\right)=\mathrm{0} \\ $$$${s}=\frac{−{k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{4}×\mathrm{5}\left({k}−\mathrm{5}\right)}}{\mathrm{2}}=\frac{−{k}\pm\left({k}−\mathrm{10}\right)}{\mathrm{2}}=−\mathrm{5},\mathrm{5}−{k} \\ $$$${s}=−\mathrm{5}\Rightarrow{Point}\:{B} \\ $$$$ \\ $$$${s}=\mathrm{5}−{k}\Rightarrow{t}^{\mathrm{2}} =\mathrm{25}−\left(\mathrm{5}−{k}\right)^{\mathrm{2}} ={k}\left(\mathrm{10}−{k}\right) \\ $$$${t}=\sqrt{{k}\left(\mathrm{10}−{k}\right)}\:\:\:\left({k}<\mathrm{10}\right) \\ $$$${A}={t}\left({s}+\mathrm{5}\right)=\sqrt{{k}\left(\mathrm{10}−{k}\right)}\left(\mathrm{10}−{k}\right)={n}\:\left({n}={integer}\left\{\right.\right. \\ $$$${k}\left(\mathrm{10}−{k}\right)\left(\mathrm{10}−{k}\right)^{\mathrm{2}} ={n}^{\mathrm{2}} \\ $$$${k}\left(\mathrm{10}−{k}\right)=\left(\frac{{n}}{\mathrm{10}−{k}}\right)^{\mathrm{2}} ={i}^{\mathrm{2}} \:\:\left({i}={integer}\right) \\ $$$${k}^{\mathrm{2}} −\mathrm{10}{k}+{i}^{\mathrm{2}} =\mathrm{0} \\ $$$${k}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}{i}^{\mathrm{2}} }}{\mathrm{2}}=\mathrm{5}\pm\sqrt{\mathrm{25}−{i}^{\mathrm{2}} } \\ $$$${i}=\mathrm{0}\Rightarrow{k}=\mathrm{0},\mathrm{10}\:\left({not}\:{ok},\:{since}\:{k}\neq\mathrm{0},{k}<\mathrm{10}\right) \\ $$$${i}=\mathrm{1}\Rightarrow{k}=\mathrm{5}\pm\sqrt{\mathrm{24}}\:\left({no}\:{integer}\right) \\ $$$${i}=\mathrm{2}\Rightarrow{k}=\mathrm{5}\pm\sqrt{\mathrm{21}}\:\left({no}\:{integer}\right) \\ $$$${i}=\mathrm{3}\Rightarrow{k}=\mathrm{5}\pm\mathrm{4}=\mathrm{1},\mathrm{9} \\ $$$${i}=\mathrm{4}\Rightarrow{k}=\mathrm{5}\pm\mathrm{3}=\mathrm{2},\mathrm{8} \\ $$$${i}=\mathrm{5}\Rightarrow{k}=\mathrm{5} \\ $$$$ \\ $$$$\Rightarrow{all}\:{possible}\:{positive}\:{integer}\:{values}\:{for}\:{k} \\ $$$${are}\:\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{8},\mathrm{9}. \\ $$
Commented by Joel576 last updated on 29/Mar/17
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *