A-particle-moving-on-the-inside-surface-of-fixed-spherical-bolw-of-radius-2-m-It-describes-a-horizontal-circle-at-distance-of-6-5-m-below-the-centre-of-the-bowl-a-find-the-speed-of-the-partic

Question Number 136109 by physicstutes last updated on 18/Mar/21

A particle moving on the inside surface of fixed spherical bolw of

radius 2 m . It describes a horizontal circle at distance of \frac{6}{5} m below

the centre of the bowl .

(a) find the speed of the particle

(b)) the period of the motion

Answered by mr W last updated on 18/Mar/21

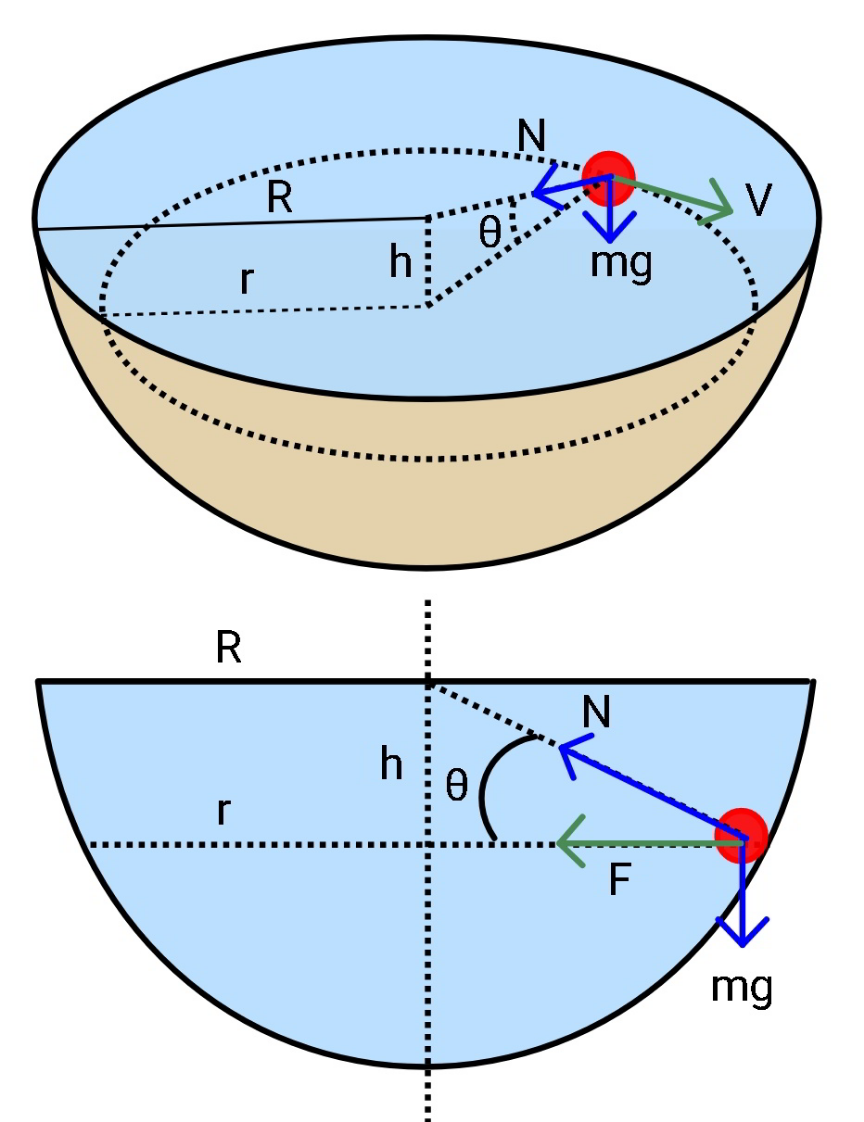
Commented by mr W last updated on 18/Mar/21

R = 2 m, h = \frac{6}{5} = 1.2 m

r = \sqrt{R^{2} - h^{2}} = 1.6 m

\tan θ = \frac{h}{r}

F = \frac{m g}{\tan θ} = \frac{{m v}^{2}}{r}

\Rightarrow v = \sqrt{\frac{g r}{\tan θ}} = \sqrt{\frac{g (R^{2} - h^{2})}{h}} = \sqrt{\frac{10 \times (2^{2} - 1 . 2^{2})}{1.2}} = 4.62 m / s

p e r i o d :

T = \frac{2 π r}{v} = 2 π \sqrt{\frac{h}{g}} = 2 π \sqrt{\frac{1.2}{10}} = 2.18 s

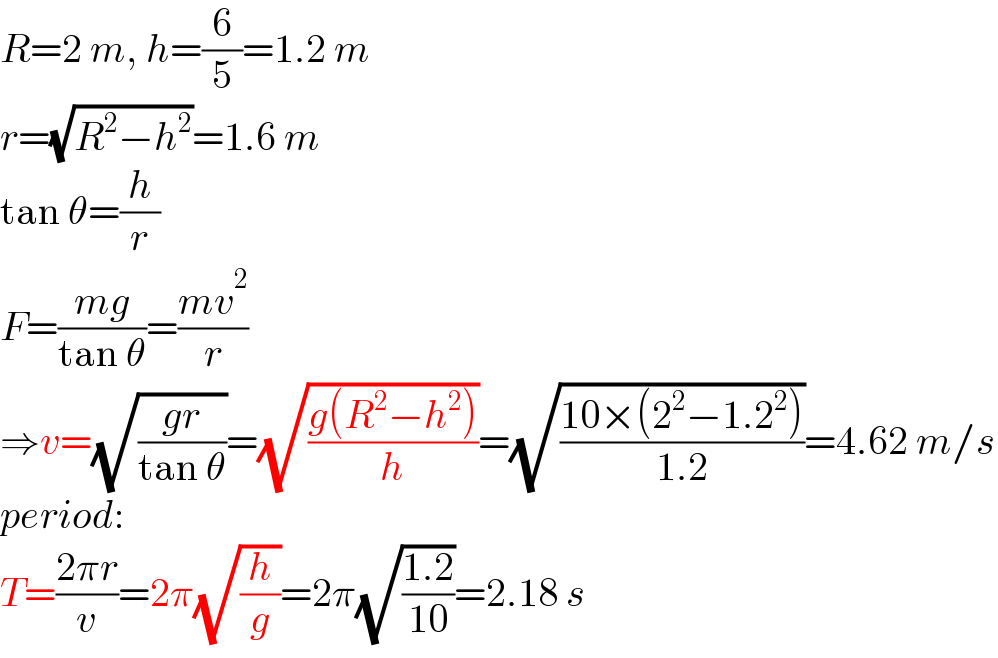
Commented by physicstutes last updated on 19/Mar/21

thank you, just a little doubt, can these problem

be solved with the angle θ being form between

downward vertical or must θ be formed between horizontal ?

Commented by mr W last updated on 19/Mar/21

c e r t a i n l y y o u c a n a l s o u s e t h e a n g l e

t o t h e v e r t i c a l .

Commented by otchereabdullai@gmail.com last updated on 19/Mar/21

wow!