Question Number 11759 by Joel576 last updated on 31/Mar/17
$$\mathrm{A}\:\mathrm{quadrilateral}\:\mathrm{with}\:\mathrm{consecutive}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{lenght}\:\mathrm{7},\:\mathrm{15},\:\mathrm{15},\:\mathrm{and}\:{d} \\ $$$$\mathrm{is}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{its}\:\mathrm{diameter}\:{d}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{circle} \\ $$
Answered by ajfour last updated on 31/Mar/17
Commented by ajfour last updated on 31/Mar/17
$${AB}=\mathrm{7}\:;\:\:\:\:{BC}=\mathrm{15};\:\:\:{CD}=\mathrm{15}; \\ $$$${AD}=\:{d}\:=\mathrm{2}{r} \\ $$$${OM}=\:\frac{\mathrm{7}}{\mathrm{2}}\:\:\:{midpoint}\:{theorem}. \\ $$$${CM}=\:\left({r}−\frac{\mathrm{7}}{\mathrm{2}}\right)\:\:;\:\:\:\:{DM}=\:\frac{\sqrt{\mathrm{4}{r}^{\mathrm{2}} \:−\mathrm{49}}}{\mathrm{2}} \\ $$$${CM}^{\mathrm{2}} \:+\:{DM}^{\mathrm{2}} \:=\:{CD}^{\mathrm{2}} \\ $$$$\left({r}−\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} +\:\left(\frac{\mathrm{4}{r}^{\mathrm{2}} \:−\mathrm{49}}{\mathrm{4}}\right)\:=\:\mathrm{225} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} −\mathrm{7}{r}\:−\mathrm{225}\:=\mathrm{0} \\ $$$${r}\:=\frac{\mathrm{7}\pm\sqrt{\mathrm{49}+\mathrm{1800}}}{\mathrm{4}}\:\:{and}\:{as}\:{r}>\mathrm{0}\:, \\ $$$${r}=\:\frac{\mathrm{7}+\mathrm{43}}{\mathrm{4}}\:=\:\frac{\mathrm{25}}{\mathrm{2}}\:. \\ $$$$ \\ $$
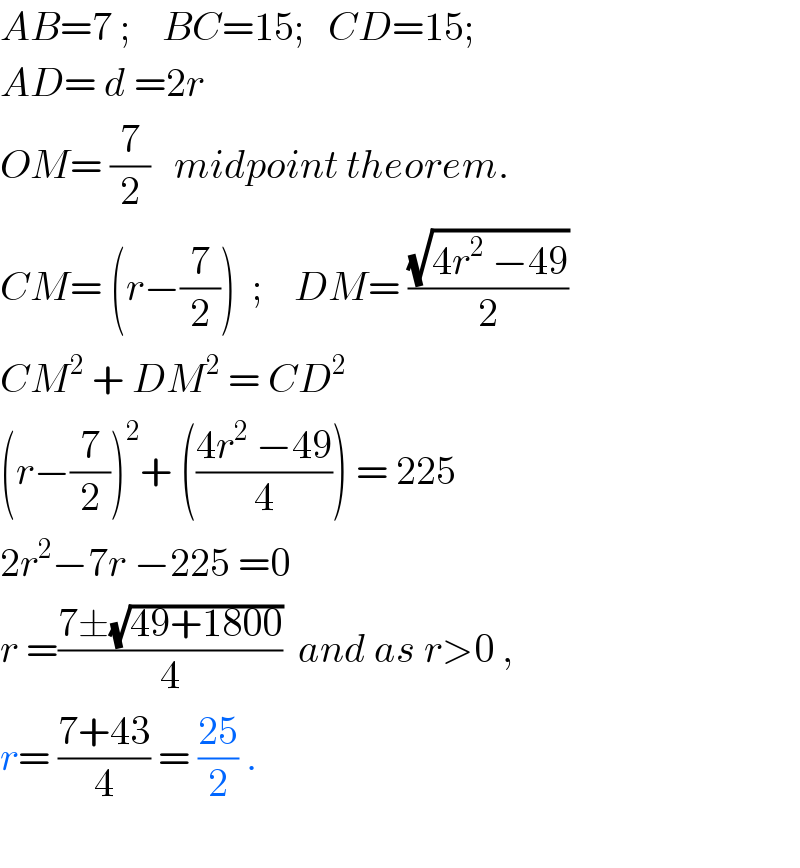
Commented by Joel576 last updated on 31/Mar/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by Joel576 last updated on 01/Apr/17
$$\mathrm{but}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{know}\:\mathrm{that}\:\mathrm{point}\:{C},\:{M},\:{O} \\ $$$$\mathrm{in}\:\mathrm{one}\:\mathrm{line}\:? \\ $$
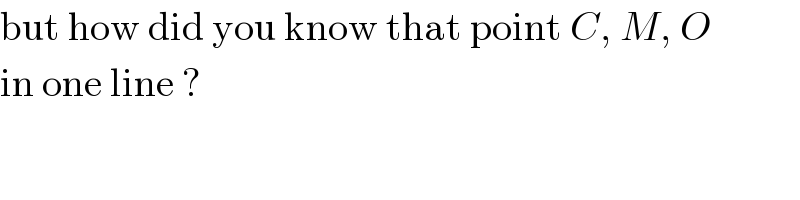
Commented by ajfour last updated on 01/Apr/17
$$\bigtriangleup{CBD}\:{is}\:{isosceles}\:{so}\:{perpendicular} \\ $$$${from}\:{C}\:{on}\:{BD}\:{bisects}\:{it}.{A}\:{line}\: \\ $$$${perpendicular}\:{to}\:{BD}\:{from}\:{center} \\ $$$${of}\:{circle}\:{even}\:{bisects}\:{its}\:{chord}\:{BD}. \\ $$
Commented by mrW1 last updated on 01/Apr/17
$${what}'{s}\:{the}\:{result}\:{if}\:{the}\:{sides}\:{are}\:\mathrm{15},\mathrm{7},\mathrm{15}\:{and}\:{d}? \\ $$
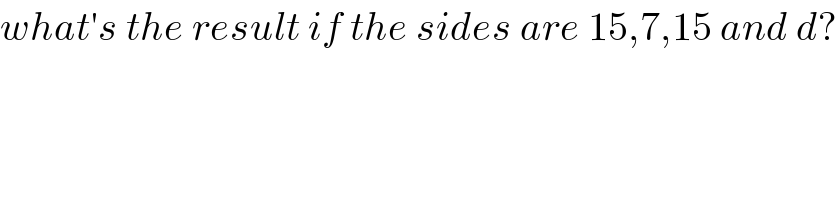
Commented by ajfour last updated on 01/Apr/17
$${the}\:{same}. \\ $$