Question Number 9603 by tawakalitu last updated on 20/Dec/16

$$\mathrm{A}\:\mathrm{regular}\:\mathrm{hexagon}\:\mathrm{has}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{lenght}\:\mathrm{8}\:\mathrm{cm}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{perpendicular}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{two} \\ $$$$\mathrm{opposite}\:\mathrm{faces}. \\ $$
Answered by mrW last updated on 20/Dec/16
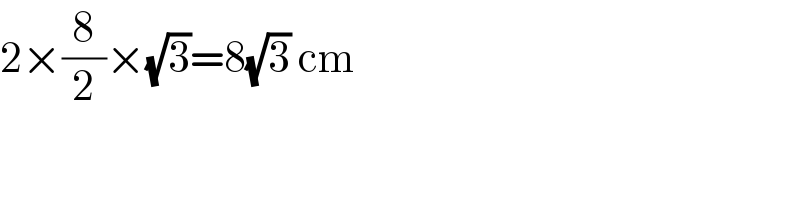
$$\mathrm{2}×\frac{\mathrm{8}}{\mathrm{2}}×\sqrt{\mathrm{3}}=\mathrm{8}\sqrt{\mathrm{3}}\:\mathrm{cm} \\ $$
Commented by tawakalitu last updated on 20/Dec/16
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 20/Dec/16

Commented by sandy_suhendra last updated on 20/Dec/16

$$\mathrm{OC}=\sqrt{\mathrm{8}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }=\sqrt{\mathrm{48}}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\mathrm{distance}\:\mathrm{between}\:\mathrm{two}\:\mathrm{opposite}\:\mathrm{faces}=\mathrm{2OC}=\mathrm{8}\sqrt{\mathrm{3}}\:\: \\ $$
Commented by tawakalitu last updated on 20/Dec/16

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
