A-string-AB-of-lenght-2l-has-a-particle-attached-to-its-midpoint-C-The-ends-A-and-B-of-the-string-are-fastened-to-two-fixed-points-with-A-distance-l-vertically-above-B-With-both-parts-of-the-string-

Question Number 137787 by physicstutes last updated on 06/Apr/21

A string A B of lenght 2 l has a particle attached to its midpoint C .

The ends A and B of the string are fastened to two fixed points

with A distance l vertically above B . With both parts of the string

taunt, the particle describes a horizontal circle about the line A B with

constant angular speed ω . If the tension in C A is three times

that in C B, prove that the angular velocity is 2 \sqrt{\frac{g}{l}} .

Answered by mr W last updated on 06/Apr/21

Commented by mr W last updated on 06/Apr/21

A B = B C = C A = l

r = l \cos 30 °

T_{1} = 3 T_{2} a s g i v e n

i n Y - d i r e c t i o n :

T_{1} \sin 30 ° = m g + T_{2} \sin 30 °

3 T_{2} \sin 30 ° = m g + T_{2} \sin 30 °

2 T_{2} \sin 30 ° = m g

\Rightarrow T_{2} = m g

\Rightarrow T_{1} = 3 m g

i n X - d i r e c t i o n :

m r ω^{2} = T_{1} \cos 30 ° + T_{2} \cos 30 ° = 4 m g \cos 30 °

m l \cos 30 ° ω^{2} = 4 m g \cos 30 °

l ω^{2} = 4 g

\Rightarrow ω = 2 \sqrt{\frac{g}{l}}

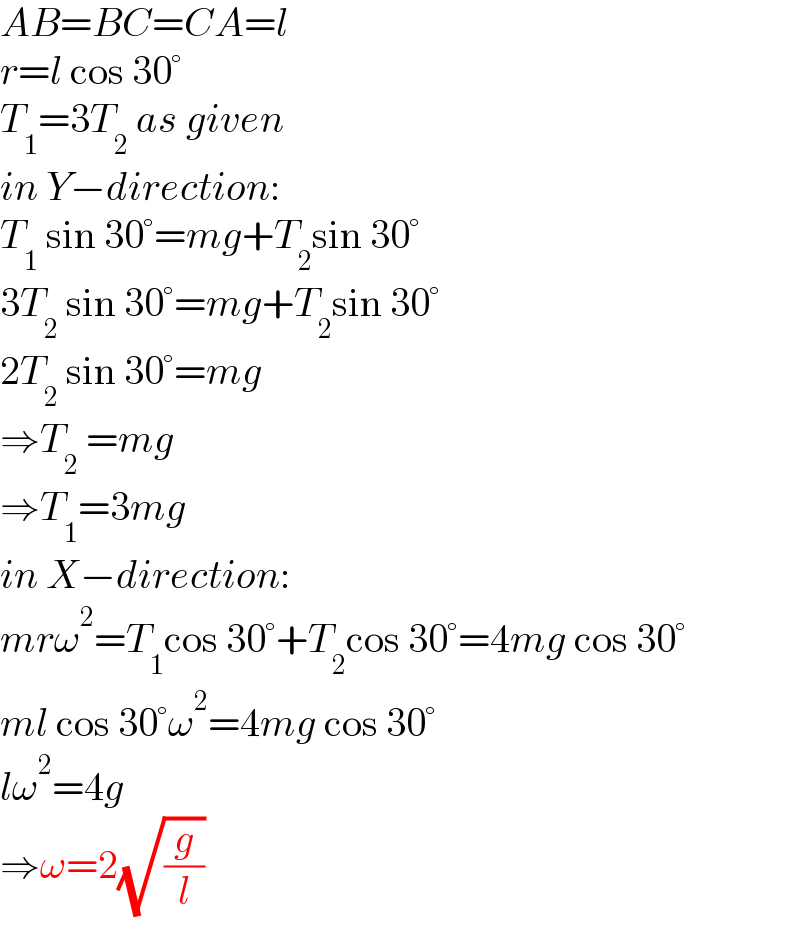
Commented by physicstutes last updated on 06/Apr/21

this is fantastic sir, i had never thought this is

an equilaterial triangle . Thank you so much sir

Commented by mr W last updated on 07/Apr/21

Facebook Tweet Pin