Menu Close

A-x-ln-y-x-y-ln-z-x-z-ln-x-y-

Tinku Tara 0 Comments
Pin




Question Number 143963 by SOMEDAVONG last updated on 20/Jun/21
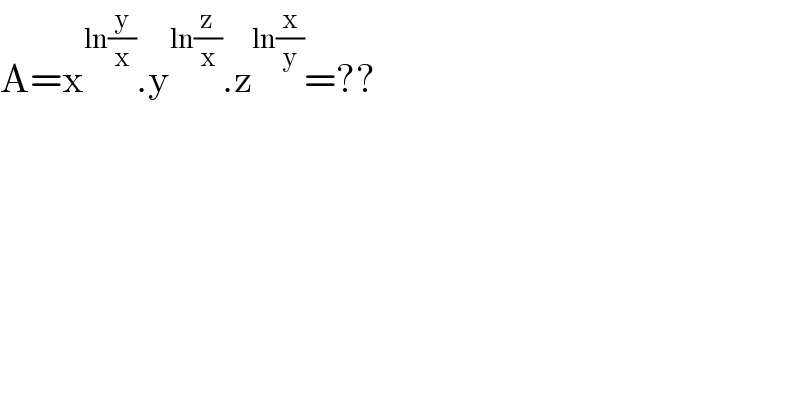
A=x^(ln(y/x)) .y^(ln(z/x)) .z^(ln(x/y)) =??
$$\mathrm{A}=\mathrm{x}^{\mathrm{ln}\frac{\mathrm{y}}{\mathrm{x}}} .\mathrm{y}^{\mathrm{ln}\frac{\mathrm{z}}{\mathrm{x}}} .\mathrm{z}^{\mathrm{ln}\frac{\mathrm{x}}{\mathrm{y}}} =?? \\ $$
Answered by Olaf_Thorendsen last updated on 20/Jun/21
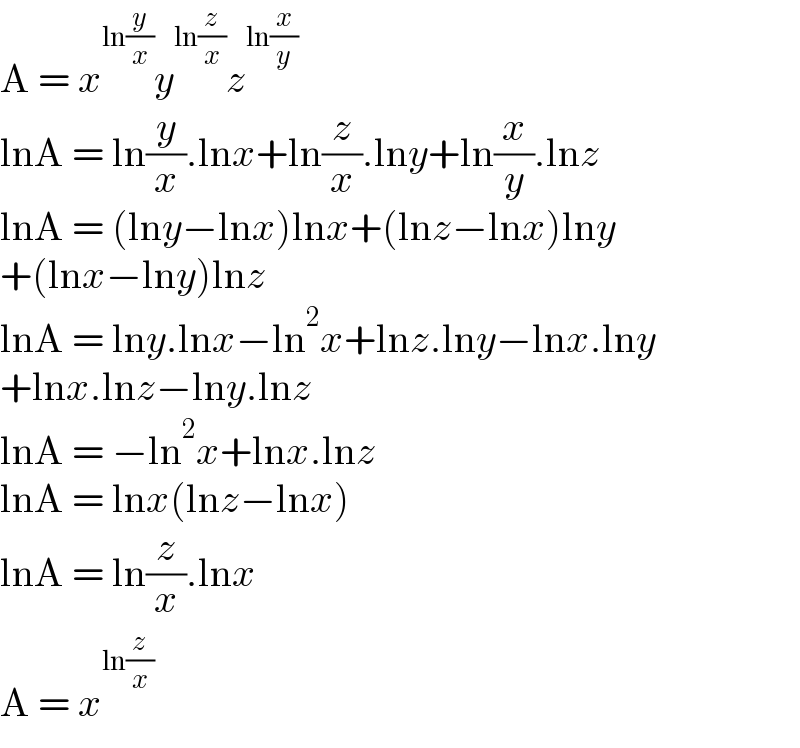
A = x^(ln(y/x)) y^(ln(z/x)) z^(ln(x/y)) lnA = ln(y/x).lnx+ln(z/x).lny+ln(x/y).lnz lnA = (lny−lnx)lnx+(lnz−lnx)lny +(lnx−lny)lnz lnA = lny.lnx−ln^2 x+lnz.lny−lnx.lny +lnx.lnz−lny.lnz lnA = −ln^2 x+lnx.lnz lnA = lnx(lnz−lnx) lnA = ln(z/x).lnx A = x^(ln(z/x))
$$\mathrm{A}\:=\:{x}^{\mathrm{ln}\frac{{y}}{{x}}} {y}^{\mathrm{ln}\frac{{z}}{{x}}} {z}^{\mathrm{ln}\frac{{x}}{{y}}} \\ $$$$\mathrm{lnA}\:=\:\mathrm{ln}\frac{{y}}{{x}}.\mathrm{ln}{x}+\mathrm{ln}\frac{{z}}{{x}}.\mathrm{ln}{y}+\mathrm{ln}\frac{{x}}{{y}}.\mathrm{ln}{z} \\ $$$$\mathrm{lnA}\:=\:\left(\mathrm{ln}{y}−\mathrm{ln}{x}\right)\mathrm{ln}{x}+\left(\mathrm{ln}{z}−\mathrm{ln}{x}\right)\mathrm{ln}{y} \\ $$$$+\left(\mathrm{ln}{x}−\mathrm{ln}{y}\right)\mathrm{ln}{z} \\ $$$$\mathrm{lnA}\:=\:\mathrm{ln}{y}.\mathrm{ln}{x}−\mathrm{ln}^{\mathrm{2}} {x}+\mathrm{ln}{z}.\mathrm{ln}{y}−\mathrm{ln}{x}.\mathrm{ln}{y} \\ $$$$+\mathrm{ln}{x}.\mathrm{ln}{z}−\mathrm{ln}{y}.\mathrm{ln}{z} \\ $$$$\mathrm{lnA}\:=\:−\mathrm{ln}^{\mathrm{2}} {x}+\mathrm{ln}{x}.\mathrm{ln}{z} \\ $$$$\mathrm{lnA}\:=\:\mathrm{ln}{x}\left(\mathrm{ln}{z}−\mathrm{ln}{x}\right) \\ $$$$\mathrm{lnA}\:=\:\mathrm{ln}\frac{{z}}{{x}}.\mathrm{ln}{x} \\ $$$$\mathrm{A}\:=\:{x}^{\mathrm{ln}\frac{{z}}{{x}}} \\ $$
Commented by SOMEDAVONG last updated on 21/Jun/21
Thanks Teacher
$$\:\: \\ $$$$\mathrm{Thanks}\:\mathrm{Teacher} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *