Question Number 131785 by faysal last updated on 08/Feb/21
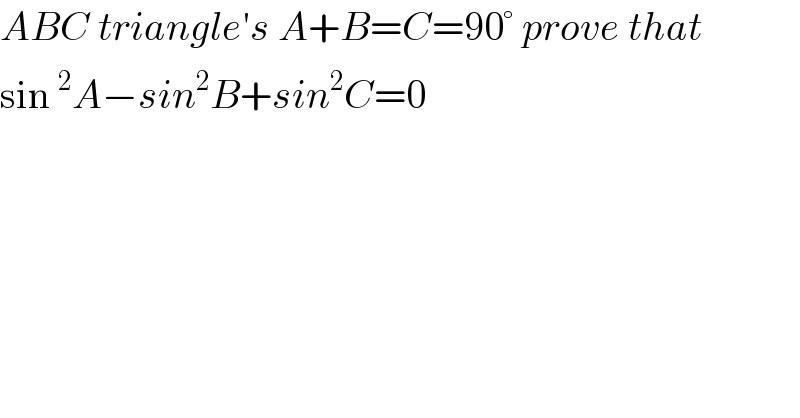
$${ABC}\:{triangle}'{s}\:{A}+{B}={C}=\mathrm{90}°\:{prove}\:{that} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {B}+{sin}^{\mathrm{2}} {C}=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Feb/21
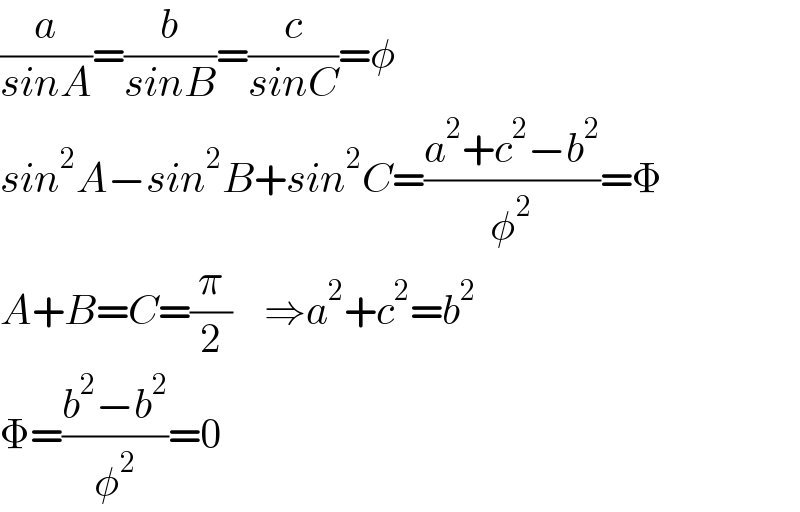
$$\frac{{a}}{{sinA}}=\frac{{b}}{{sinB}}=\frac{{c}}{{sinC}}=\phi \\ $$$${sin}^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {B}+{sin}^{\mathrm{2}} {C}=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\phi^{\mathrm{2}} }=\Phi \\ $$$${A}+{B}={C}=\frac{\pi}{\mathrm{2}}\:\:\:\:\Rightarrow{a}^{\mathrm{2}} +{c}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Phi=\frac{{b}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\phi^{\mathrm{2}} }=\mathrm{0} \\ $$
