Menu Close

ABCD-EFGH-is-cube-X-is-midpoint-EF-if-AB-6-cm-how-distance-AX-to-BD-

Tinku Tara 0 Comments
Pin




Question Number 2499 by Syaka last updated on 21/Nov/15
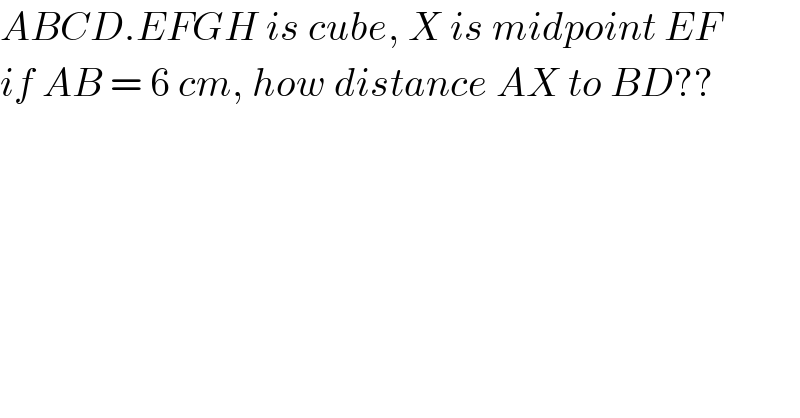
ABCD.EFGH is cube, X is midpoint EF if AB = 6 cm, how distance AX to BD??
$${ABCD}.{EFGH}\:{is}\:{cube},\:{X}\:{is}\:{midpoint}\:{EF} \\ $$$${if}\:{AB}\:=\:\mathrm{6}\:{cm},\:{how}\:{distance}\:{AX}\:{to}\:{BD}?? \\ $$
Commented by prakash jain last updated on 21/Nov/15
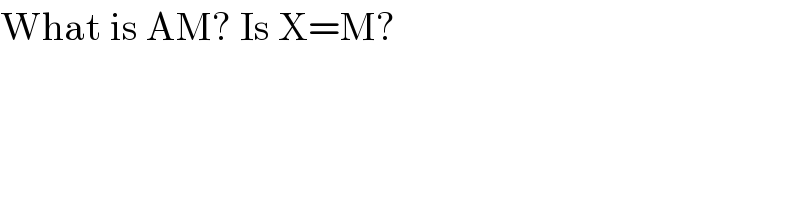
What is AM? Is X=M?
$$\mathrm{What}\:\mathrm{is}\:\mathrm{AM}?\:\mathrm{Is}\:\mathrm{X}=\mathrm{M}? \\ $$
Commented by Syaka last updated on 21/Nov/15
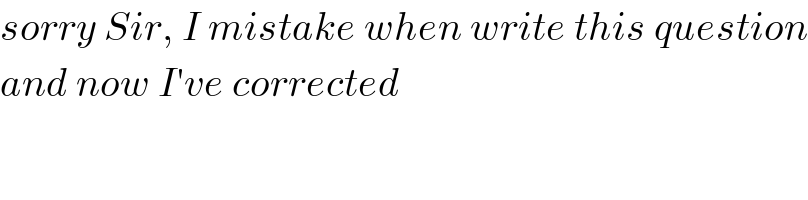
sorry Sir, I mistake when write this question and now I′ve corrected
$${sorry}\:{Sir},\:{I}\:{mistake}\:{when}\:{write}\:{this}\:{question} \\ $$$${and}\:{now}\:{I}'{ve}\:{corrected} \\ $$
Answered by prakash jain last updated on 21/Nov/15
Let A(0,0,0) A=(0,0,0) B=(6,0,0) C=(6,6,0) D=(0,6,0) E=(0,0,6) F=(6,0,6) G=(6,6,6) H=(0,6,6) X=(3,0,6) direction vector d_1 ^→ =BD^(→) =(−6,6,0) BD: ((x−6)/(−6))=(y/6)=t, z=0 x=6−6t, y=6t, z=0 (some point Q on line BD) direction vector d_2 ^→ =AX^(→) =(3,0,6) AX: (x/3)=(z/6)=s, y=0 x=3s, z=6s, y=0 (some point R on line AX) QR^(→) =(3s−6+6t,−6t,6s) To calculate the distance we need to solve for s and t such QR^(→) ⊥BD^(→) and QR^(→) ⊥AX^(→) . QR^(→) •BD^(→) =0 and QR^(→) •AX^(→) =0 Once s and t are found we can find coordinates of Q and R and calculate the distance. QR^(→) •BD^(→) =0 ⇒−18s+36−36t−36t=0 s+4t=2 ....(1) QR^(→) •AX^(→) =0 ⇒9s−18+18t+36s=0 5s+2t=2 ....(2) From(1) and (2) t=(4/9),s=(2/9) x=6−((24)/9)=((10)/3), y=(8/3), z=0 ( point Q on line BD) x=(2/3), z=(4/3), y=0 (point R on line AX) QR^(→) is ⊥ to both BD and AX and hence its length gives the distance. QR=(√(((8/3))^2 +((8/3))^2 +((4/3))^2 ))=(1/3)(√(128+16))=4
$$\mathrm{Let}\:\mathrm{A}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{A}=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:\mathrm{B}=\left(\mathrm{6},\mathrm{0},\mathrm{0}\right)\:\mathrm{C}=\left(\mathrm{6},\mathrm{6},\mathrm{0}\right)\:\mathrm{D}=\left(\mathrm{0},\mathrm{6},\mathrm{0}\right) \\ $$$$\mathrm{E}=\left(\mathrm{0},\mathrm{0},\mathrm{6}\right)\:\mathrm{F}=\left(\mathrm{6},\mathrm{0},\mathrm{6}\right)\:\mathrm{G}=\left(\mathrm{6},\mathrm{6},\mathrm{6}\right)\:\mathrm{H}=\left(\mathrm{0},\mathrm{6},\mathrm{6}\right) \\ $$$$\mathrm{X}=\left(\mathrm{3},\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{direction}\:\mathrm{vector}\:\overset{\rightarrow} {{d}}_{\mathrm{1}} =\overset{\rightarrow} {\mathrm{BD}}=\left(−\mathrm{6},\mathrm{6},\mathrm{0}\right) \\ $$$$\mathrm{BD}:\:\:\:\frac{{x}−\mathrm{6}}{−\mathrm{6}}=\frac{{y}}{\mathrm{6}}={t},\:{z}=\mathrm{0} \\ $$$${x}=\mathrm{6}−\mathrm{6}{t},\:{y}=\mathrm{6}{t},\:{z}=\mathrm{0}\:\left(\mathrm{some}\:{point}\:{Q}\:\mathrm{on}\:\mathrm{line}\:\mathrm{BD}\right) \\ $$$$\mathrm{direction}\:\mathrm{vector}\:\overset{\rightarrow} {{d}}_{\mathrm{2}} =\overset{\rightarrow} {\mathrm{AX}}=\left(\mathrm{3},\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{AX}:\:\frac{{x}}{\mathrm{3}}=\frac{{z}}{\mathrm{6}}={s},\:{y}=\mathrm{0}\: \\ $$$${x}=\mathrm{3}{s},\:{z}=\mathrm{6}{s},\:{y}=\mathrm{0}\:\:\:\:\left(\mathrm{some}\:\mathrm{point}\:\mathrm{R}\:\mathrm{on}\:\mathrm{line}\:\mathrm{AX}\right) \\ $$$$\overset{\rightarrow} {\mathrm{QR}}=\left(\mathrm{3}{s}−\mathrm{6}+\mathrm{6}{t},−\mathrm{6}{t},\mathrm{6}{s}\right) \\ $$$$\mathrm{To}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{for}\:{s}\:\mathrm{and}\:{t}\:\mathrm{such}\:\overset{\rightarrow} {\mathrm{QR}}\bot\overset{\rightarrow} {\mathrm{BD}}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{QR}}\bot\overset{\rightarrow} {\mathrm{AX}}. \\ $$$$\overset{\rightarrow} {\mathrm{QR}}\bullet\overset{\rightarrow} {\mathrm{BD}}\:=\mathrm{0}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{QR}}\bullet\overset{\rightarrow} {\mathrm{AX}}=\mathrm{0} \\ $$$$\mathrm{Once}\:{s}\:\mathrm{and}\:{t}\:\mathrm{are}\:\mathrm{found}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{coordinates} \\ $$$$\mathrm{of}\:\mathrm{Q}\:\mathrm{and}\:\mathrm{R}\:\mathrm{and}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{distance}. \\ $$$$\overset{\rightarrow} {\mathrm{QR}}\bullet\overset{\rightarrow} {\mathrm{BD}}\:=\mathrm{0}\:\Rightarrow−\mathrm{18}{s}+\mathrm{36}−\mathrm{36}{t}−\mathrm{36}{t}=\mathrm{0} \\ $$$${s}+\mathrm{4}{t}=\mathrm{2}\:\:\:\:\:\:\:….\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\overset{\rightarrow} {\mathrm{QR}}\bullet\overset{\rightarrow} {\mathrm{AX}}\:=\mathrm{0}\:\Rightarrow\mathrm{9}{s}−\mathrm{18}+\mathrm{18}{t}+\mathrm{36}{s}=\mathrm{0} \\ $$$$\mathrm{5}{s}+\mathrm{2}{t}=\mathrm{2}\:\:\:\:\:….\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:{t}=\frac{\mathrm{4}}{\mathrm{9}},{s}=\frac{\mathrm{2}}{\mathrm{9}} \\ $$$${x}=\mathrm{6}−\frac{\mathrm{24}}{\mathrm{9}}=\frac{\mathrm{10}}{\mathrm{3}},\:{y}=\frac{\mathrm{8}}{\mathrm{3}},\:{z}=\mathrm{0}\:\left(\:{point}\:{Q}\:\mathrm{on}\:\mathrm{line}\:\mathrm{BD}\right) \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}},\:{z}=\frac{\mathrm{4}}{\mathrm{3}},\:{y}=\mathrm{0}\:\:\:\:\left(\mathrm{point}\:\mathrm{R}\:\mathrm{on}\:\mathrm{line}\:\mathrm{AX}\right) \\ $$$$\overset{\rightarrow} {\mathrm{QR}}\:\mathrm{is}\:\bot\:\mathrm{to}\:\mathrm{both}\:\mathrm{BD}\:\mathrm{and}\:\mathrm{AX}\:\mathrm{and}\:\mathrm{hence}\:\mathrm{its} \\ $$$$\mathrm{length}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{distance}. \\ $$$$\mathrm{QR}=\sqrt{\left(\frac{\mathrm{8}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{8}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{128}+\mathrm{16}}=\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *