Question Number 139419 by mathocean1 last updated on 26/Apr/21

$${ABCD}\:{is}\:{a}\:{rectangle}\:{such}\:{that}\: \\ $$$${AD}=\mathrm{2}{AB}\:{and}\:{its}\:{center}\:{is}\:{O}.\: \\ $$$${H}\:{is}\:{the}\:{top}\:{of}\:{a}\:{pyramid}\:{which} \\ $$$${has}\:{ABCD}\:{as}\:{base}.\:{All}\:{lateral} \\ $$$${faces}\:{are}\:{isosceles}\:{triangles}.\:{planes} \\ $$$$\left({HAB}\right)\:{and}\:\left({HCD}\right)\:{are}\:\bot. \\ $$$${i}\:{have}\:{joined}\:{a}\:{graphic}. \\ $$$$\mathrm{1}.\:{show}\:{that}\:\left({OH}\right)\bot\left({ABC}\right). \\ $$$$\mathrm{2}.\:{show}\:{that}\:{OH}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{AB} \\ $$$$ \\ $$
Commented by mathocean1 last updated on 26/Apr/21

Commented by mr W last updated on 26/Apr/21

$${OH}={AB}\neq\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{AB} \\ $$
Commented by mr W last updated on 27/Apr/21

Commented by mr W last updated on 27/Apr/21

Commented by mr W last updated on 27/Apr/21
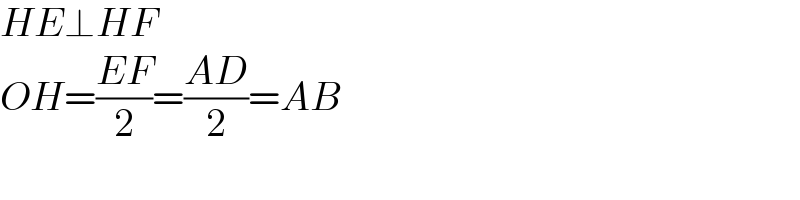
$${HE}\bot{HF} \\ $$$${OH}=\frac{{EF}}{\mathrm{2}}=\frac{{AD}}{\mathrm{2}}={AB} \\ $$
