advanced-calculus-0-pi-2-x-tan-x-1-2-dx-

Question Number 136572 by mnjuly1970 last updated on 23/Mar/21

\dots . a d v a n c e d c a l c u l u s \dots .

\boldsymbol ϕ = \int_{0}^{\frac{π}{2}} x . {(t a n (x))}^{\frac{1}{2}} d x = ? ?

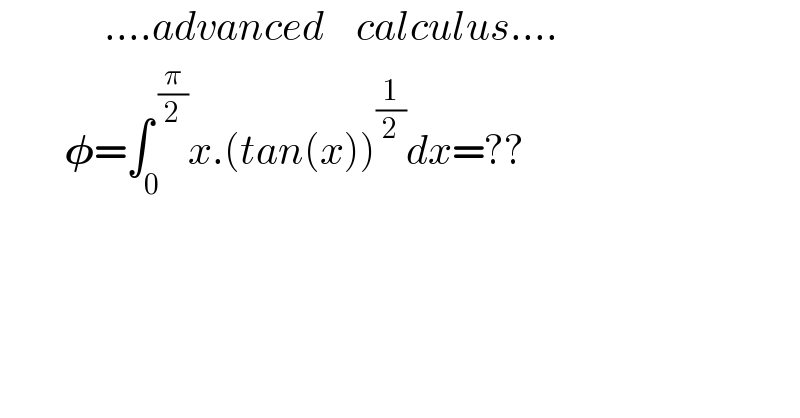
Commented by Olaf last updated on 24/Mar/21

Do you know if it can be calculated

sir ? I can calculate \int_{0}^{\frac{π}{2}} \sqrt{\tan x} d x

but not \int_{0}^{\frac{π}{2}} x \sqrt{\tan x} d x

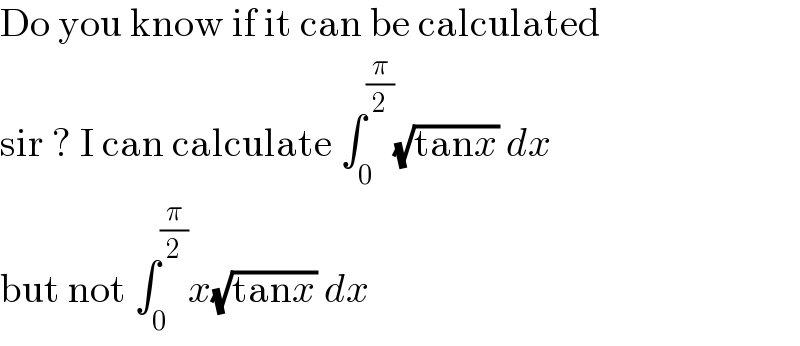
Answered by Dwaipayan Shikari last updated on 24/Mar/21

\int_{0}^{\frac{π}{2}} x \sqrt{t a n x} d x \int_{0}^{\frac{π}{2}} \sqrt{t a n x} d x = \frac{Γ (\frac{3}{4}) Γ (\frac{1}{4})}{2 Γ (1)} = \frac{π}{\sqrt{2}}

= \frac{π}{2} (\frac{π}{\sqrt{2}}) - \int_{0}^{\frac{π}{2}} \int \sqrt{t a n x} d x

\int \sqrt{t a n x} d x = 2 \int \frac{t^{2}}{1 + t^{4}} d t = \frac{1}{\sqrt{i}} {t a n}^{- 1} (\frac{t}{\sqrt{i}}) - \frac{1}{\sqrt{- i}} {t a n}^{- 1} (\frac{t}{\sqrt{- i}})

= \frac{π^{2}}{2 \sqrt{2}} - \int_{0}^{\frac{π}{2}} \frac{1}{\sqrt{i}} {t a n}^{- 1} (\frac{t}{\sqrt{i}}) - \frac{1}{\sqrt{- i}} {t a n}^{- 1} (\frac{t}{\sqrt{- i}}) d t

= \frac{π^{2}}{2 \sqrt{2}} - \frac{π}{2} (e^{- \frac{π}{4} i} {t a n}^{- 1} \frac{π}{2 \sqrt{i}} - e^{\frac{π}{4} i} {t a n}^{- 1} \frac{π}{2 \sqrt{- i}}) + \frac{1}{2 i} l o g (\frac{4 i - π^{2}}{4 i + π^{2}})

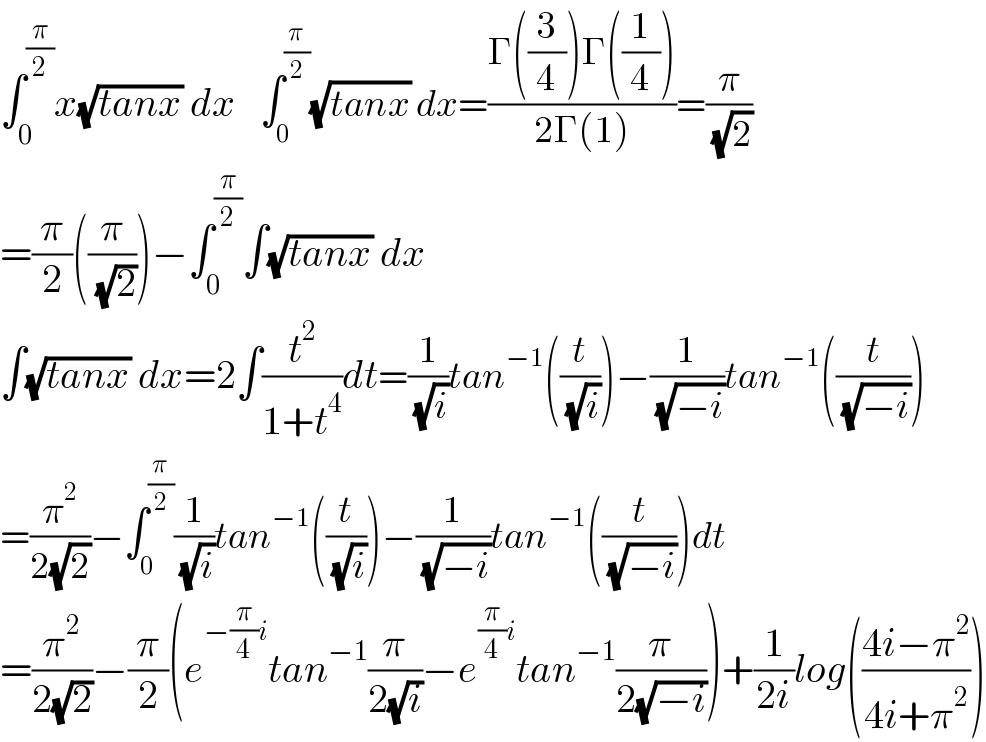
Commented by mnjuly1970 last updated on 24/Mar/21

t h a n k s a l o t m r p a y a n \dots g r a t e f u l . .

Answered by Ñï= last updated on 24/Mar/21

ϕ = \int_{0}^{π / 2} x \sqrt{\tan x} d x = 2 \int_{0}^{\infty} \frac{t^{2}}{1 + t^{4}} \tan^{- 1} t^{2} d t

ϕ (s) = 2 \int_{0}^{\infty} \frac{t^{2}}{1 + t^{4}} \tan^{- 1} ({s t}^{2}) d t

ϕ {(s)}^{'} = 2 \int_{0}^{\infty} \frac{t^{4}}{(1 + t^{4}) (1 + s^{2} t^{4})} d t = 2 \int_{0}^{\infty} (\frac{1}{1 + s^{2} t^{4}} - \frac{1}{1 + t^{4}}) \frac{1}{1 - s^{2}} d t

= \frac{2}{1 - s^{2}} \int_{0}^{\infty} {\frac{s^{- 1 / 2}}{4} \cdot \frac{u^{- 3 / 4}}{1 + u} - \frac{1}{4} \cdot \frac{u^{- 3 / 4}}{1 + u}} d u

= \frac{1}{2 (1 - s^{2})} (s^{- 1 / 2} - 1) Γ (\frac{1}{4}) Γ (\frac{3}{4})

= \frac{π}{\sqrt{2} (1 - s^{2})} (s^{- 1 / 2} - 1)

ϕ (1) = \frac{π}{\sqrt{2}} \int_{0}^{1} \frac{s^{- 1 / 2} - 1}{1 - s^{2}} d s \overset{s^{1 / 2} \to s}{=} \frac{π}{\sqrt{2}} \int_{0}^{1} (\frac{1}{1 + s} + \frac{1 - s}{1 + s^{2}}) d s = \frac{π}{\sqrt{2}} (\frac{1}{2} l n 2 + \frac{π}{4})

Commented by mnjuly1970 last updated on 24/Mar/21

t h a n k s a l o t \dots .

v e r y n i c e s i r ? ? ?

Commented by Ñï= last updated on 24/Mar/21

t h e o t h e r p e o p l e d i d i t . i u p l o a d p i c t u r e, b u t n o t d i s p l a y .

Commented by mnjuly1970 last updated on 24/Mar/21

m e r c e y \dots t h a n k y o u s o m u c h . .

Answered by maths mind last updated on 24/Mar/21

f (a, b) = \int_{0}^{π} \frac{c o s (a x)}{{s i n}^{b} (x)} d x = \int_{0}^{π} 2^{\boldsymbol b - 1} \boldsymbol i^{\boldsymbol b} \frac{\boldsymbol e^{\boldsymbol i a x} + \boldsymbol e^{- \boldsymbol i a x}}{{(1 - \boldsymbol e^{- 2 \boldsymbol i x})}^{\boldsymbol b}} . \boldsymbol e^{- \boldsymbol i b x} \boldsymbol d x

= 2^{\boldsymbol b - 1} \boldsymbol i^{\boldsymbol b} \int_{0}^{π} \frac{e^{i (a - b) x} + e^{- i (a + b) x}}{{(1 - e^{- 2 i x})}^{b}} d x

l e t g (s) = \int_{0}^{π} \frac{e^{i s x}}{{(1 - e^{- 2 i x})}^{b}} d x =

\frac{1}{{(1 - e^{- 2 i x})}^{b}} = 1 + \sum_{n ⩾ 1} \frac{\underset{k = 0}{\prod^{n - 1}} (b + k)}{n!} e^{- 2 i n x}

g (s) = \int_{0}^{π} e^{i s x} d x + \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} \int_{0}^{π} e^{x (- 2 i n + i s)} d x

= \frac{e^{i s π} - 1}{i s} + \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} . \frac{e^{i π s} - 1}{- 2 i n + i s}

f (a, b) = 2^{b - 1} i^{b} (g (i (a - b)) + g (- i (a + b)))

= 2^{b - 1} . i^{b - 1} (\frac{\boldsymbol e^{\boldsymbol i (\boldsymbol a - \boldsymbol b) \boldsymbol π} - 1}{a - \boldsymbol b} + \frac{e^{- i (a + b)} - 1}{- a - b})

+ \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} . \frac{1 - e^{i π (a - \boldsymbol b)}}{2 \boldsymbol n + \boldsymbol b - a} + \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} . \frac{1 - e^{i π (- a - b)}}{2 n + a + b}

= 2^{b - 1} i^{b - 1} (\frac{1}{b - a} + \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} . \frac{1}{2 (n + \frac{(b - a)}{2})}) (1 - e^{i π (a - b)}) +

2^{b - 1} i^{b - 1} (\frac{1}{a + b} + \sum_{n ⩾ 1} \frac{{(b)}_{n}}{n!} . \frac{1}{2 (n + \frac{(a + b)}{2})}) (- e^{- i π (a + b)} + 1)

= 2^{b - 1} i^{b - 1} (\frac{1}{b - a} + \sum_{n ⩾ 1} \frac{{(b)}_{n} {(\frac{b - a}{2})}_{n}}{(a - b) (\frac{- a + b + 2}{2})}) (- e^{i π (a - b)} + 1)

+ 2^{b - 1} i^{b - 1} (\frac{1}{a + b} + \sum_{n ⩾ 1} \frac{{(b)}_{n} {(\frac{a + b}{2})}_{n}}{(a + b) {(\frac{a + b + 2}{2})}_{n}}) (- e^{- i π (a + b)} + 1)

= 2^{b - 1} i^{b - 1} ._{2} F_{1} (b, \frac{b - a}{2}; \frac{b - a + 2}{2}; 1) . \frac{1 - e^{i π (a - b)}}{b - a}

+ 2^{b - 1} i^{b - 1} ._{2} F_{1} (b, \frac{a + b}{2}; \frac{a + b + 2}{2}; 1) . \frac{1 - e^{- i π (a + b)}}{a + b}

_{2} F_{1} (a, b; c, 1) = \frac{Γ (c) Γ (c - a - b)}{Γ (c - a) Γ (c - b)}

w r g e t 2^{b - 1} i^{b - 1} (\frac{Γ (\frac{b - a + 2}{2}) Γ (1 - b)}{Γ (1 - \frac{a}{2} - \frac{b}{2})}) \frac{1 - e^{i π (a - b)}}{b - a}

+ 2^{b - 1} i^{b - 1} (\frac{Γ (\frac{a + b + 2}{2}) Γ (1 - b)}{Γ (1 + \frac{a - b}{2})}) . \frac{1 - \boldsymbol e^{- \boldsymbol i π (a + b)}}{a + b}

= 2^{b - 1} i^{b - 1} . \frac{Γ (1 - b) Γ (\frac{a + b}{2})}{Γ (1 + \frac{a - b}{2})} . \frac{1 - e^{- \boldsymbol i π (a + b)}}{2} + \frac{Γ (1 - b) Γ (\frac{b - a}{2})}{Γ (1 - \frac{a + b}{2})} . \frac{1 - e^{i π (a - b)}}{2}

= 2^{b - 1} . i^{b - 1} (\frac{Γ (1 - b)}{Γ (1 + \frac{a - b}{2}) Γ (1 - \frac{a + b}{2})} . i π e^{- i \frac{π}{2} (a + b)})

+ 2^{b - 1} i^{b - 1} (\frac{Γ (1 - b)}{Γ (1 + \frac{a - b}{2}) Γ (1 - \frac{a + b}{2})} . i π e^{i \frac{π}{2} (\frac{a - b}{2})})

= 2^{b - 1} . \frac{Γ (1 - b) . 2 π c o s (\frac{π a}{2})}{Γ (1 + \frac{a - b}{2}) Γ (1 - \frac{a + b}{2})} = π \frac{2^{b} c o s (\frac{π a}{2}) Γ (1 - b)}{Γ (1 + \frac{a - b}{2}) Γ (1 - \frac{a + b}{2})}

ϕ = \int_{0}^{\frac{π}{2}} x \sqrt{t g (x)} d x = \sqrt{2} \int_{0}^{π} \frac{x s i n (x)}{\sqrt{s i n (2 x)}} d x

= \frac{1}{2 \sqrt{2}} \int_{0}^{\frac{π}{2}} \frac{y s i n (\frac{y}{2})}{\sqrt{s i n (y)}}

f (a, b) = \int_{0}^{π} \frac{c o s (a x)}{{s i n}^{b} (x)} d x, \partial^{a} f (a, b) = \int_{0}^{π} \frac{- x s i n (a x)}{{s i n}^{b} (x)} d x

(a, b) = (\frac{1}{2}; \frac{1}{2}) w e g e t ϕ = - \frac{1}{2 \sqrt{2}} \frac{\partial f}{\partial a} (\frac{1}{2}; \frac{1}{2}) = \frac{π}{4 s i n (\frac{π}{4})} (Ψ (\frac{1}{2}) - Ψ (\frac{1}{4}))

= \frac{π}{2 \sqrt{2}} (- 2 l n (2) - \boldsymbol γ + \frac{π}{2} + 3 l n (2) + γ) = \frac{π^{2}}{4 \sqrt{2}} + \frac{π l n (2)}{2 \sqrt{2}} = \int_{0}^{\frac{π}{2}} x \sqrt{t a n (x)} d x

Commented by mnjuly1970 last updated on 24/Mar/21

t h a n k y o u s o m u c h . .

t h a n k y o u s o m u c h . .