Menu Close

advanced-calculus-0-x-b-1-1-x-a-s-dx-b-a-s-b-a-a-s-

Tinku Tara
Pin




Question Number 131104 by mnjuly1970 last updated on 01/Feb/21
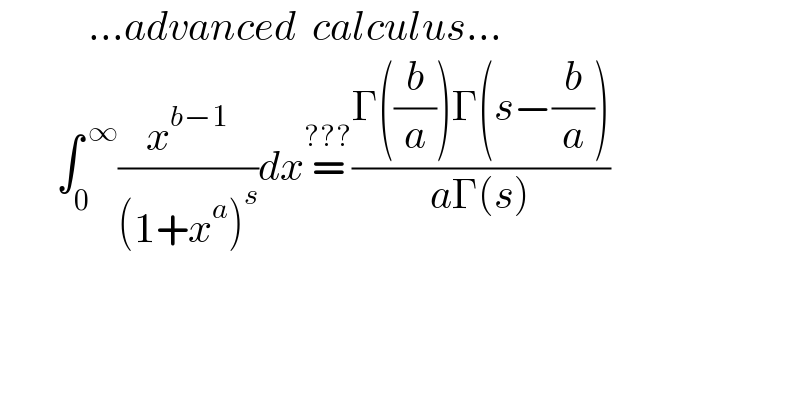
...advanced calculus... ∫_0 ^( ∞) (x^(b−1) /((1+x^a )^s ))dx=^(???) ((Γ((b/a))Γ(s−(b/a)))/(aΓ(s)))
$$\:\:\:\:\:\:\:\:\:\:\:…{advanced}\:\:{calculus}… \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{b}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{{a}} \right)^{{s}} }{dx}\overset{???} {=}\frac{\Gamma\left(\frac{{b}}{{a}}\right)\Gamma\left({s}−\frac{{b}}{{a}}\right)}{{a}\Gamma\left({s}\right)} \\ $$
Answered by Ar Brandon last updated on 01/Feb/21
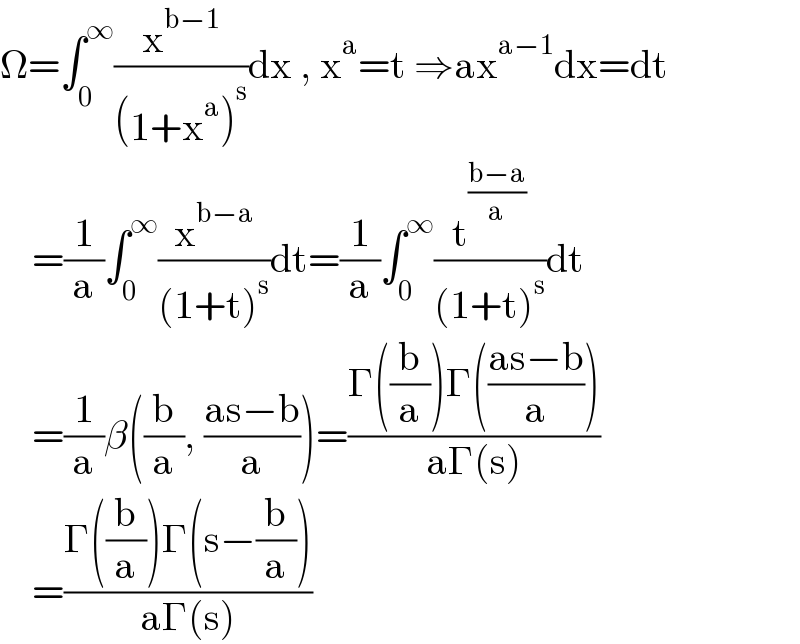
Ω=∫_0 ^∞ (x^(b−1) /((1+x^a )^s ))dx , x^a =t ⇒ax^(a−1) dx=dt =(1/a)∫_0 ^∞ (x^(b−a) /((1+t)^s ))dt=(1/a)∫_0 ^∞ (t^((b−a)/a) /((1+t)^s ))dt =(1/a)β((b/a), ((as−b)/a))=((Γ((b/a))Γ(((as−b)/a)))/(aΓ(s))) =((Γ((b/a))Γ(s−(b/a)))/(aΓ(s)))
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{b}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{a}} \right)^{\mathrm{s}} }\mathrm{dx}\:,\:\mathrm{x}^{\mathrm{a}} =\mathrm{t}\:\Rightarrow\mathrm{ax}^{\mathrm{a}−\mathrm{1}} \mathrm{dx}=\mathrm{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{b}−\mathrm{a}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{s}} }\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{b}−\mathrm{a}}{\mathrm{a}}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{s}} }\mathrm{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{a}}\beta\left(\frac{\mathrm{b}}{\mathrm{a}},\:\frac{\mathrm{as}−\mathrm{b}}{\mathrm{a}}\right)=\frac{\Gamma\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\Gamma\left(\frac{\mathrm{as}−\mathrm{b}}{\mathrm{a}}\right)}{\mathrm{a}\Gamma\left(\mathrm{s}\right)} \\ $$$$\:\:\:\:=\frac{\Gamma\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\Gamma\left(\mathrm{s}−\frac{\mathrm{b}}{\mathrm{a}}\right)}{\mathrm{a}\Gamma\left(\mathrm{s}\right)} \\ $$
Commented by mnjuly1970 last updated on 01/Feb/21
thank you mr brandon..
$${thank}\:{you}\:{mr}\:{brandon}.. \\ $$
Commented by Ar Brandon last updated on 01/Feb/21
With pleasure Sir��

Pin