advanced-calculus-find-the-value-of-n-1-1-n-H-2n-n-

Question Number 138145 by mnjuly1970 last updated on 10/Apr/21

\dots \dots \dots . . a d v a n c e d \dots \dots \dots c a l c u l u s \dots \dots \dots

f i n d t h e v a l u e o f ::

Θ = \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n} H_{2 n}}{n} = ? ? ?

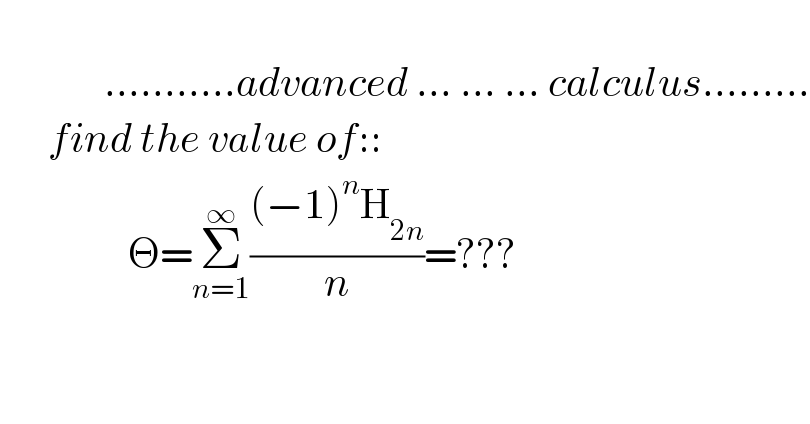
Answered by Dwaipayan Shikari last updated on 10/Apr/21

\underset{n = 1}{\sum^{\infty}} H_{2 n} x^{2 n} = H_{2} x^{2} + H_{4} x^{4} + H_{6} x^{6} + H_{8} x^{8} + \dots = ψ (x^{2})

A n d \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n} H_{2 n}}{n} = \int_{0}^{1} \frac{ψ (- x)}{\sqrt{x}} d x

\underset{n = 1}{\sum^{\infty}} H_{n} x^{n} = H_{1} x + H_{2} x^{2} + H_{3} x^{3} + \dots = - \frac{l o g (1 - x)}{1 - x}

\underset{n = 1}{\sum^{\infty}} {(- 1)}^{n} H_{n} x^{n} = - H_{1} x + H_{2} x^{2} - H_{3} x^{3} + \dots = - \frac{l o g (1 + x)}{1 + x}

ψ (x^{2}) = - \frac{1}{2} (\frac{l o g (1 - x)}{1 - x} + \frac{l o g (1 + x)}{1 + x})

ψ (x) = - \frac{1}{2} (\frac{l o g (1 - \sqrt{x})}{1 - \sqrt{x}} + \frac{l o g (1 + \sqrt{x})}{1 + \sqrt{x}})

\int_{0}^{1} \frac{ψ (- x)}{\sqrt{x}} = - \frac{1}{2} \int_{0}^{1} \frac{1}{i \sqrt{x}} (\frac{l o g (1 - i \sqrt{x})}{1 - i \sqrt{x}} + \frac{l o g (1 + i \sqrt{x})}{1 + i \sqrt{x}}) d x x = t^{2}

= - \frac{1}{2 i} \int_{0}^{1} \frac{l o g (1 - i t)}{1 - i t} + \frac{l o g (1 + i t)}{1 + i t} d t

= - \frac{1}{2 i} \int_{0}^{1} \frac{l o g (1 + t^{2})}{1 + t^{2}} + i t l o g (\frac{1 - i t}{1 + i t}) d t

\dots .

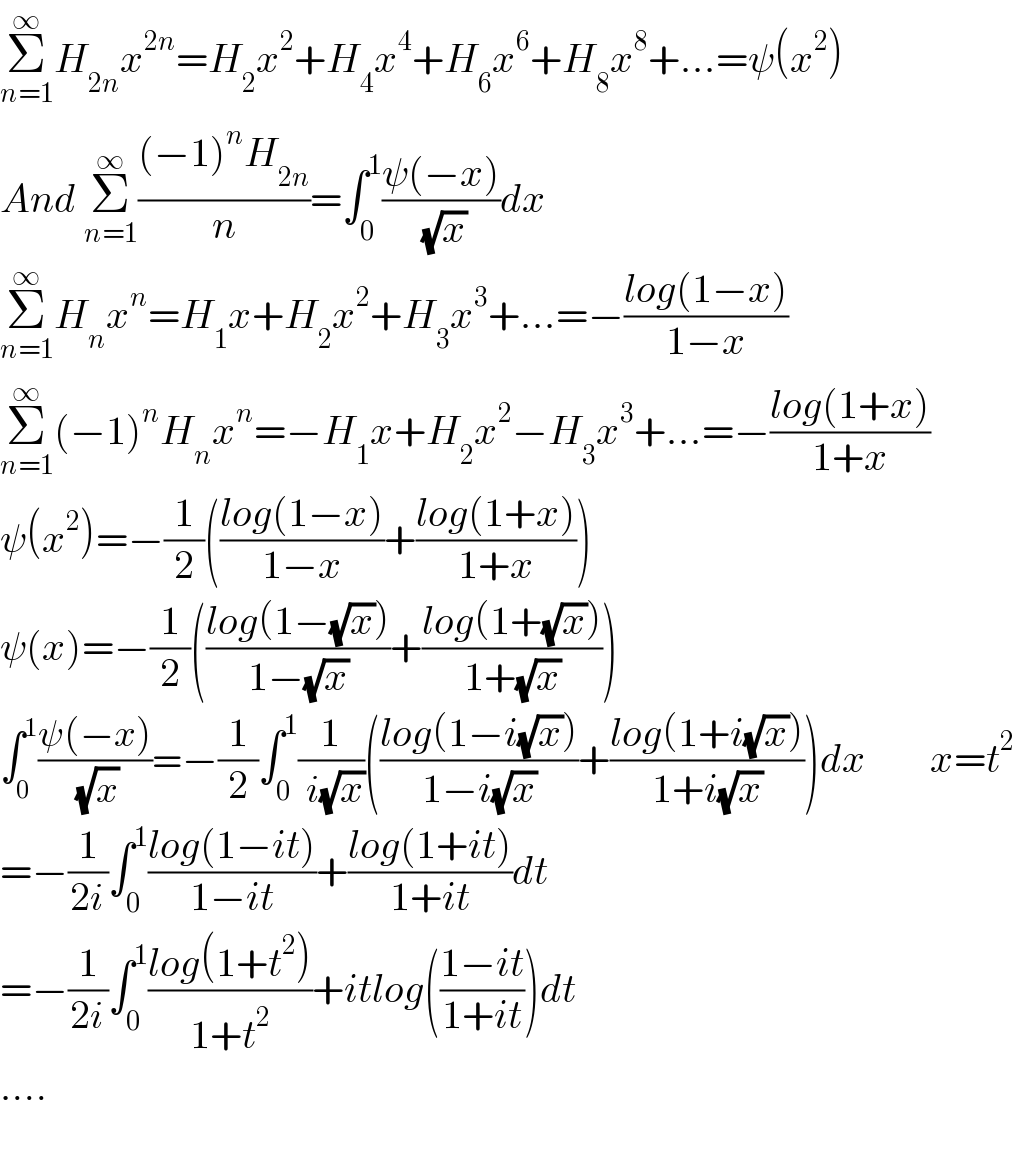
Commented by mnjuly1970 last updated on 10/Apr/21

g r a t e f u l f o r y o u r a t t e n t i o n

a n d e f f o r t \dots

Answered by Ñï= last updated on 10/Apr/21

\underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n}}{n} H_{2 n} = - \int_{0}^{1} \frac{1}{1 - u} \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n} x^{n} (1 - u^{2 n}) d u x = 1

= \int_{0}^{1} \frac{1}{u - 1} \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n} [x^{n} - {({x u}^{2})}^{n}] d u

= \int_{0}^{1} \frac{1}{u - 1} [l n (1 + x) - l n (1 + {x u}^{2})] d u

= \dots . . ? ? ?

Commented by mnjuly1970 last updated on 10/Apr/21

t h a n k s a l o t m r \dots

Answered by mnjuly1970 last updated on 10/Apr/21

f (x) := \underset{n = 1}{\sum^{\infty}} \frac{H_{n}}{n} x^{n} = \frac{1}{2} {l n}^{2} (1 - x) + {l i}_{2} (x)

f (i) := Σ \frac{H_{n}}{n} {(i)}^{n} = \frac{1}{2} {l n}^{2} (1 - i) + {l i}_{2} (i) \dots . (*)

f (- i) := \underset{n = 1}{\sum^{\infty}} \frac{H_{n}}{n} {(- i)}^{n} = \frac{1}{2} {l n}^{2} (1 + i) + {l i}_{2} (- i) \dots . (* *)

(*) + (* *) : Σ \frac{H_{n}}{n} (i^{n} + {(- i)}^{n}) = \frac{1}{2} {{l n}^{2} (\sqrt{2} e^{\frac{- i π}{4}}) + {l n}^{2} (\sqrt{2} e^{\frac{i π}{4}})} + \frac{1}{2} {l i}_{2} (i^{2})

∴ \underset{n = 1}{\sum^{\infty}} \frac{H_{2 n}}{2 n} ({(- 1)}^{n} + {(- 1)}^{n}) = \frac{1}{2} {{(l n (\sqrt{2}) - \frac{i π}{4})}^{2} + {(l n (\sqrt{2}) + \frac{i π}{4})}^{2}} - \frac{π^{2}}{24}

= \frac{1}{2} {2 (\frac{1}{4} {l n}^{2} (2) - \frac{π^{2}}{16})} - \frac{π^{2}}{24}

∴ Θ = \frac{1}{4} {l n}^{2} (2) - \frac{5 π^{2}}{48} \dots ✓ ✓

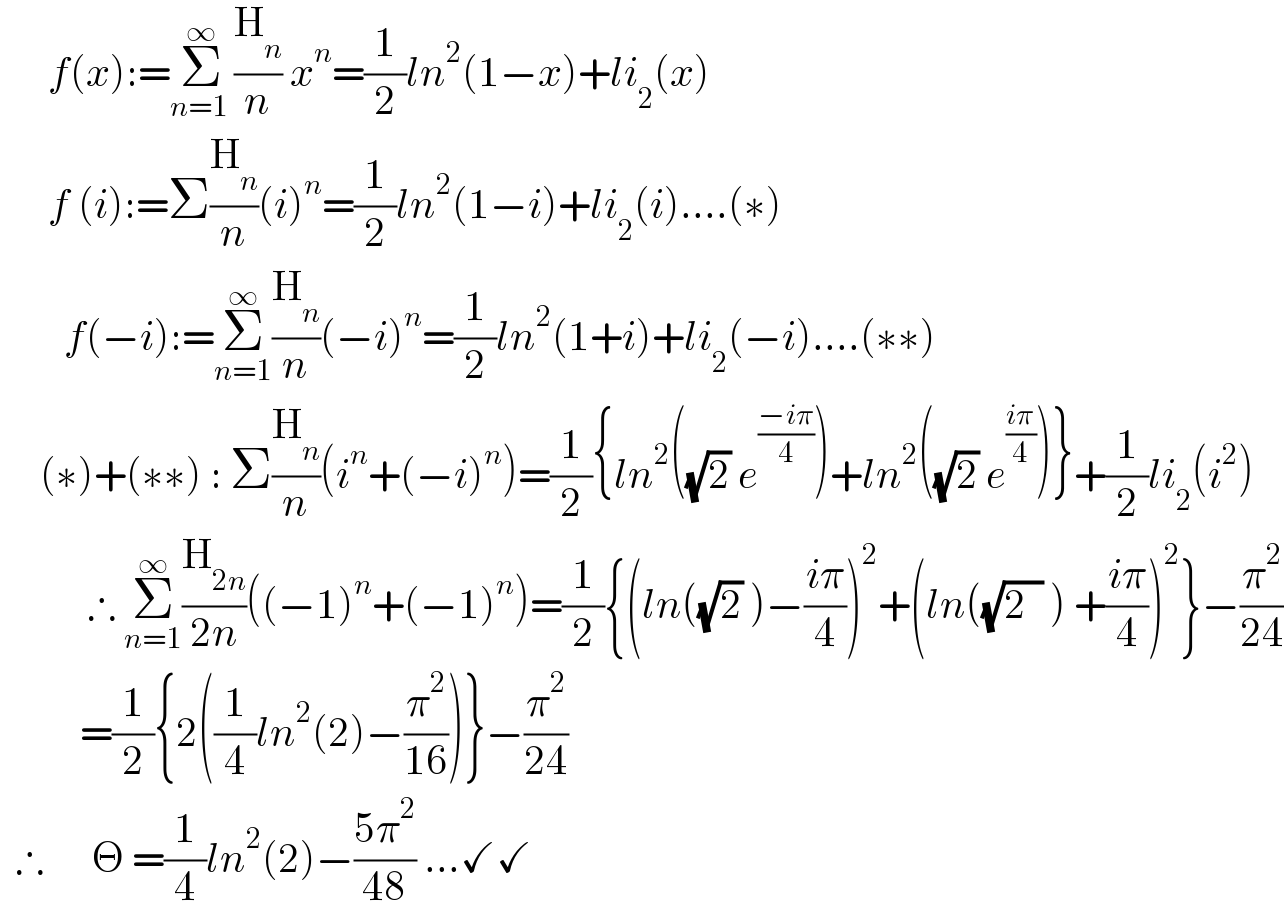
Answered by Kamel last updated on 10/Apr/21

Commented by Kamel last updated on 10/Apr/21

W i t h o u t c o m p l e x n u m b e r s .

Commented by mnjuly1970 last updated on 10/Apr/21

t h a n k s a l o t . .