Question Number 141649 by mnjuly1970 last updated on 21/May/21
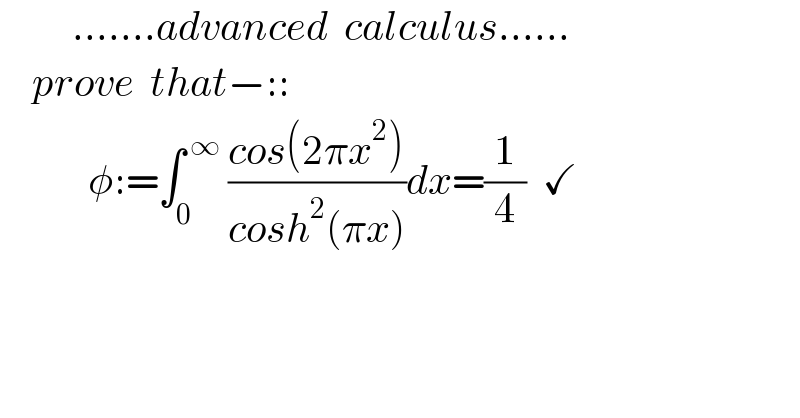
$$\:\:\:\:\:\:\:\:\:…….{advanced}\:\:{calculus}…… \\ $$$$\:\:\:\:{prove}\:\:{that}−:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\phi:=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{cos}\left(\mathrm{2}\pi{x}^{\mathrm{2}} \right)}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\checkmark \\ $$
Answered by ArielVyny last updated on 22/May/21
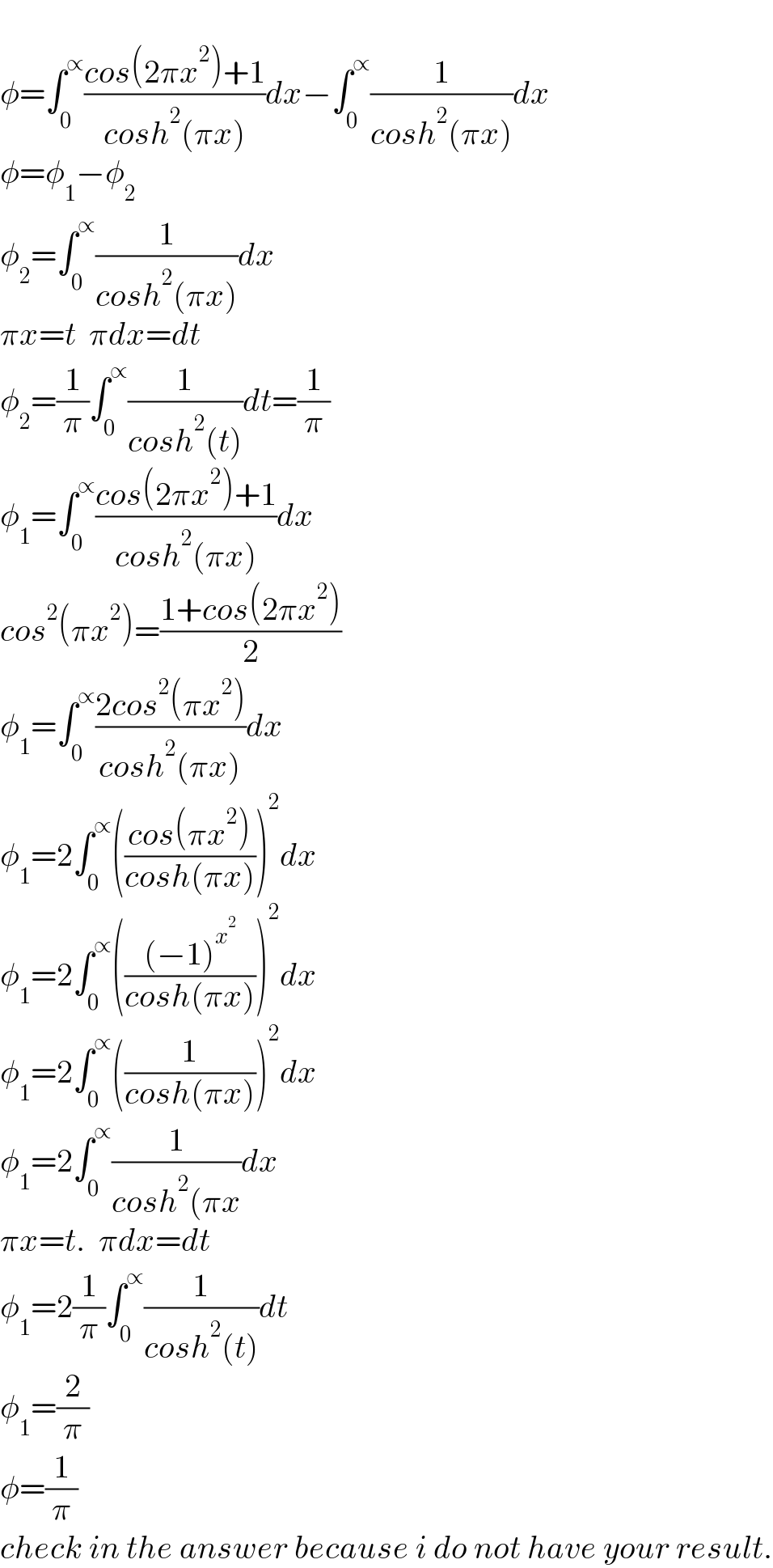
$$ \\ $$$$\phi=\int_{\mathrm{0}} ^{\propto} \frac{{cos}\left(\mathrm{2}\pi{x}^{\mathrm{2}} \right)+\mathrm{1}}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx}−\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx} \\ $$$$\phi=\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \\ $$$$\phi_{\mathrm{2}} =\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx}\:\: \\ $$$$\pi{x}={t}\:\:\pi{dx}={dt} \\ $$$$\phi_{\mathrm{2}} =\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{{cosh}^{\mathrm{2}} \left({t}\right)}{dt}=\frac{\mathrm{1}}{\pi} \\ $$$$\phi_{\mathrm{1}} =\int_{\mathrm{0}} ^{\propto} \frac{{cos}\left(\mathrm{2}\pi{x}^{\mathrm{2}} \right)+\mathrm{1}}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx} \\ $$$${cos}^{\mathrm{2}} \left(\pi{x}^{\mathrm{2}} \right)=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$\phi_{\mathrm{1}} =\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\pi{x}^{\mathrm{2}} \right)}{{cosh}^{\mathrm{2}} \left(\pi{x}\right)}{dx} \\ $$$$\phi_{\mathrm{1}} =\mathrm{2}\int_{\mathrm{0}} ^{\propto} \left(\frac{{cos}\left(\pi{x}^{\mathrm{2}} \right)}{{cosh}\left(\pi{x}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$\phi_{\mathrm{1}} =\mathrm{2}\int_{\mathrm{0}} ^{\propto} \left(\frac{\left(−\mathrm{1}\right)^{{x}^{\mathrm{2}} } }{{cosh}\left(\pi{x}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$\phi_{\mathrm{1}} =\mathrm{2}\int_{\mathrm{0}} ^{\propto} \left(\frac{\mathrm{1}}{{cosh}\left(\pi{x}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$\phi_{\mathrm{1}} =\mathrm{2}\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{{cosh}^{\mathrm{2}} \left(\pi{x}\right.}{dx} \\ $$$$\pi{x}={t}.\:\:\pi{dx}={dt} \\ $$$$\phi_{\mathrm{1}} =\mathrm{2}\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{{cosh}^{\mathrm{2}} \left({t}\right)}{dt} \\ $$$$\phi_{\mathrm{1}} =\frac{\mathrm{2}}{\pi} \\ $$$$\phi=\frac{\mathrm{1}}{\pi} \\ $$$${check}\:{in}\:{the}\:{answer}\:{because}\:{i}\:{do}\:{not}\:{have}\:{your}\:{result}. \\ $$
Commented by mnjuly1970 last updated on 22/May/21
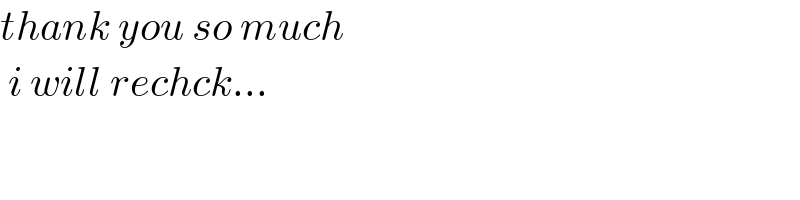
$${thank}\:{you}\:{so}\:{much} \\ $$$$\:{i}\:{will}\:{rechck}… \\ $$
