advanced-cslculus-prove-that-n-0-1-16-n-4-8n-1-2-8n-4-1-8n-5-1-8n-6-pi-

Question Number 131711 by mnjuly1970 last updated on 07/Feb/21

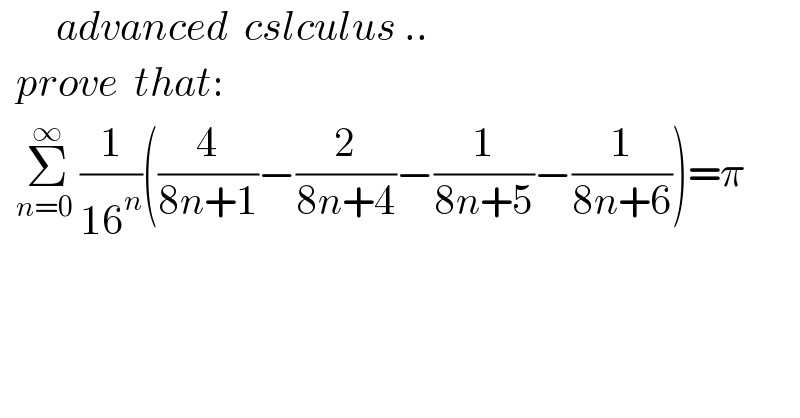
a d v a n c e d c s l c u l u s . .

p r o v e t h a t :

\underset{n = 0}{\sum^{\infty}} \frac{1}{16^{n}} (\frac{4}{8 n + 1} - \frac{2}{8 n + 4} - \frac{1}{8 n + 5} - \frac{1}{8 n + 6}) = π

Commented by JDamian last updated on 07/Feb/21

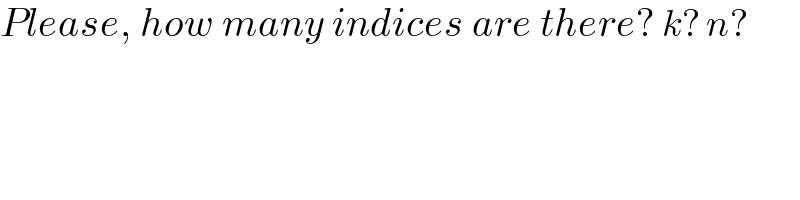
P l e a s e, h o w m a n y i n d i c e s a r e t h e r e ? k ? n ?

Facebook Tweet Pin