Menu Close

Advanced-Mathematics-Evaluate-n-1-coth-pin-n-3-

Tinku Tara 0 Comments
Pin




Question Number 143428 by mnjuly1970 last updated on 14/Jun/21
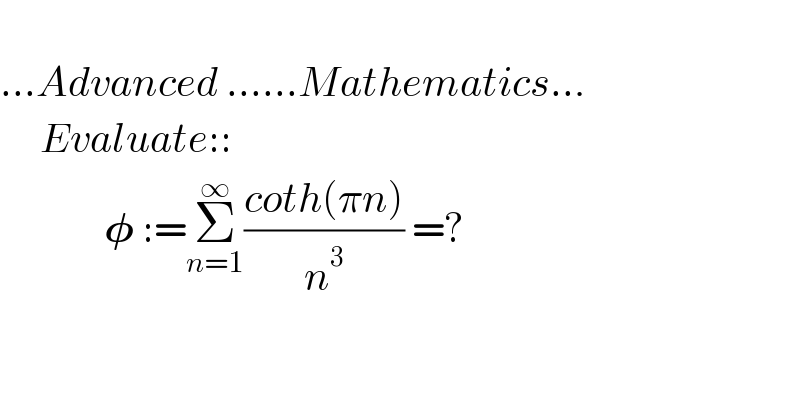
...Advanced ......Mathematics... Evaluate:: 𝛗 :=Σ_(n=1) ^∞ ((coth(πn))/n^3 ) =?
$$\:\:\:\:\: \\ $$$$…{Advanced}\:……{Mathematics}… \\ $$$$\:\:\:\:\:{Evaluate}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}\::=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left(\pi{n}\right)}{{n}^{\mathrm{3}} }\:=? \\ $$
Answered by mindispower last updated on 16/Jun/21
let f(z)=((πcoth(πz)cot(πz))/z^3 ) pols of f are {ik,k;k∈Z} let C_R :{Re^(iθ) ,θ∈[0,2π[} we use the reisidus theorem withe the fact that coth,cot are bounded ⇒ lim_(R→∞) ∫_C_R f(z)dz=0 Residue therem⇒ΣRes(f)=0 Res(f,k)=lim_(x→k) (x−k).π((coth(πx)cot(πx))/x^3 )=((coth(πk))/k^3 ),k≠0 Res(f,ik)=((coth(πk))/k^3 ),k≠0 ⇒Σ_(k∈Z−{0}) .((coth(πk))/k^3 )+Σ_(k∈Z−{0}) ((coth(πk))/k^3 )+Res(f,0)=0 ⇒4Σ_(k≥1) ((coth(πk))/k^3 )=−Res(f,0) Res(f,0) cotan(πx)=(1/(πx))−((πx)/3)−((π^3 x^3 )/(45))+0(x^3 ) coth(πx)=icot(iπx)=(1/(πx))+((πx)/3)−(π^3 /(45))x^3 Res(f,0),coeficuent of (1/x)in π((coth(πx)cot(πx))/x^3 ) =(π/x^3 )(−(π^2 /9)−2(π^2 /(45)))x^2 =−((7π^3 )/(45)) 4Σ_(n≥1) ((coth(πn))/n^3 )=−.−((7π^3 )/(45)) Σ_(n≥1) ((coth(πn))/n^3 )=((7π^3 )/(180))
$${let}\:{f}\left({z}\right)=\frac{\pi{coth}\left(\pi{z}\right){cot}\left(\pi{z}\right)}{{z}^{\mathrm{3}} } \\ $$$${pols}\:{of}\:{f}\:{are}\:\left\{{ik},{k};{k}\in\mathbb{Z}\right\} \\ $$$${let}\:{C}_{{R}} :\left\{{Re}^{{i}\theta} ,\theta\in\left[\mathrm{0},\mathrm{2}\pi\left[\right\}\right.\right. \\ $$$${we}\:{use}\:{the}\:{reisidus}\:{theorem} \\ $$$${withe}\:{the}\:{fact}\:{that}\:{coth},{cot}\:{are}\:{bounded} \\ $$$$\Rightarrow \\ $$$$\underset{{R}\rightarrow\infty} {\mathrm{lim}}\int_{{C}_{{R}} } {f}\left({z}\right){dz}=\mathrm{0} \\ $$$${Residue}\:{therem}\Rightarrow\Sigma{Res}\left({f}\right)=\mathrm{0} \\ $$$${Res}\left({f},{k}\right)=\underset{{x}\rightarrow{k}} {\mathrm{lim}}\left({x}−{k}\right).\pi\frac{{coth}\left(\pi{x}\right){cot}\left(\pi{x}\right)}{{x}^{\mathrm{3}} }=\frac{{coth}\left(\pi{k}\right)}{{k}^{\mathrm{3}} },{k}\neq\mathrm{0} \\ $$$${Res}\left({f},{ik}\right)=\frac{{coth}\left(\pi{k}\right)}{{k}^{\mathrm{3}} },{k}\neq\mathrm{0} \\ $$$$\Rightarrow\underset{{k}\in\mathbb{Z}−\left\{\mathrm{0}\right\}} {\sum}.\frac{{coth}\left(\pi{k}\right)}{{k}^{\mathrm{3}} }+\underset{{k}\in\mathbb{Z}−\left\{\mathrm{0}\right\}} {\sum}\frac{{coth}\left(\pi{k}\right)}{{k}^{\mathrm{3}} }+{Res}\left({f},\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{coth}\left(\pi{k}\right)}{{k}^{\mathrm{3}} }=−{Res}\left({f},\mathrm{0}\right) \\ $$$${Res}\left({f},\mathrm{0}\right) \\ $$$${cotan}\left(\pi{x}\right)=\frac{\mathrm{1}}{\pi{x}}−\frac{\pi{x}}{\mathrm{3}}−\frac{\pi^{\mathrm{3}} {x}^{\mathrm{3}} }{\mathrm{45}}+\mathrm{0}\left({x}^{\mathrm{3}} \right) \\ $$$${coth}\left(\pi{x}\right)={icot}\left({i}\pi{x}\right)=\frac{\mathrm{1}}{\pi{x}}+\frac{\pi{x}}{\mathrm{3}}−\frac{\pi^{\mathrm{3}} }{\mathrm{45}}{x}^{\mathrm{3}} \\ $$$${Res}\left({f},\mathrm{0}\right),{coeficuent}\:{of}\:\frac{\mathrm{1}}{{x}}{in}\:\pi\frac{{coth}\left(\pi{x}\right){cot}\left(\pi{x}\right)}{{x}^{\mathrm{3}} } \\ $$$$=\frac{\pi}{{x}^{\mathrm{3}} }\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{9}}−\mathrm{2}\frac{\pi^{\mathrm{2}} }{\mathrm{45}}\right){x}^{\mathrm{2}} =−\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{45}} \\ $$$$\mathrm{4}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{coth}\left(\pi{n}\right)}{{n}^{\mathrm{3}} }=−.−\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{45}} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{coth}\left(\pi{n}\right)}{{n}^{\mathrm{3}} }=\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{180}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *