Question Number 10475 by ketto last updated on 13/Feb/17

$${aman}\:{walks}\:\mathrm{600}{m}\:{at}\:{a}\:{bearing}\:{of}\: \\ $$$$\mathrm{45}^{\mathrm{0}\:} {then}\:\mathrm{500}{m}\:{at}\:{a}\:{bearing}\:\mathrm{90}^{\mathrm{0}} \: \\ $$$${then}\:\mathrm{300}{m}\:{at}\:{bearing}\:{of}\:\mathrm{135}^{\mathrm{0}\:} \: \\ $$$${then}\:\mathrm{400}{m}\:{at}\:{a}\:{bearing}\:{of}\:\mathrm{225}^{\mathrm{0}} \\ $$$$.{find}\:{the}\:{resultant}\:{displacement} \\ $$$${which}\:{the}\:{man}\:{has}\:{made} \\ $$
Answered by sandy_suhendra last updated on 13/Feb/17
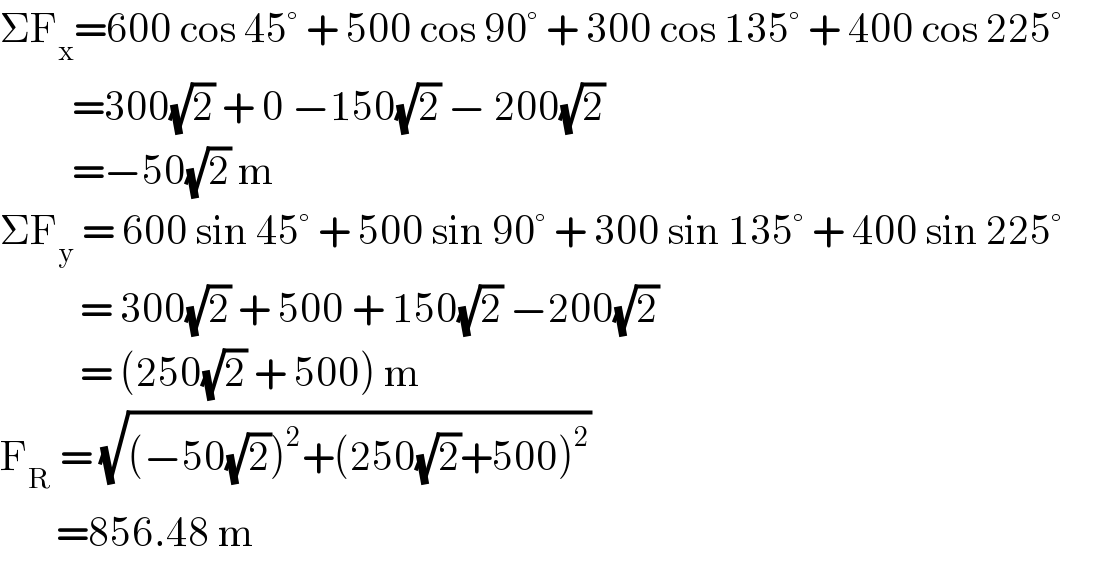
$$\Sigma\mathrm{F}_{\mathrm{x}} =\mathrm{600}\:\mathrm{cos}\:\mathrm{45}°\:+\:\mathrm{500}\:\mathrm{cos}\:\mathrm{90}°\:+\:\mathrm{300}\:\mathrm{cos}\:\mathrm{135}°\:+\:\mathrm{400}\:\mathrm{cos}\:\mathrm{225}° \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{300}\sqrt{\mathrm{2}}\:+\:\mathrm{0}\:−\mathrm{150}\sqrt{\mathrm{2}}\:−\:\mathrm{200}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{50}\sqrt{\mathrm{2}}\:\mathrm{m} \\ $$$$\Sigma\mathrm{F}_{\mathrm{y}} \:=\:\mathrm{600}\:\mathrm{sin}\:\mathrm{45}°\:+\:\mathrm{500}\:\mathrm{sin}\:\mathrm{90}°\:+\:\mathrm{300}\:\mathrm{sin}\:\mathrm{135}°\:+\:\mathrm{400}\:\mathrm{sin}\:\mathrm{225}°\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{300}\sqrt{\mathrm{2}}\:+\:\mathrm{500}\:+\:\mathrm{150}\sqrt{\mathrm{2}}\:−\mathrm{200}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{250}\sqrt{\mathrm{2}}\:+\:\mathrm{500}\right)\:\mathrm{m} \\ $$$$\mathrm{F}_{\mathrm{R}} \:=\:\sqrt{\left(−\mathrm{50}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{250}\sqrt{\mathrm{2}}+\mathrm{500}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\mathrm{856}.\mathrm{48}\:\mathrm{m} \\ $$
