Question Number 6430 by sanusihammed last updated on 27/Jun/16

$${An}\:{oil}\:{can}\:{is}\:{to}\:{be}\:{made}\:{in}\:{form}\:{of}\:{a}\:{right}\:{circular}\:{cylinder}\:{that}\:{be} \\ $$$${inscribed}\:{in}\:{a}\:{sphere}\:{of}\:{radius}\:{R}.\:{obtain}\:{the}\:{maximum}\: \\ $$$${volume}\:{of}\:{the}\:{can}. \\ $$
Commented by sanusihammed last updated on 27/Jun/16
$${Thanks}\:{so}\:{much}\:{sir}.\: \\ $$
Commented by Yozzii last updated on 27/Jun/16
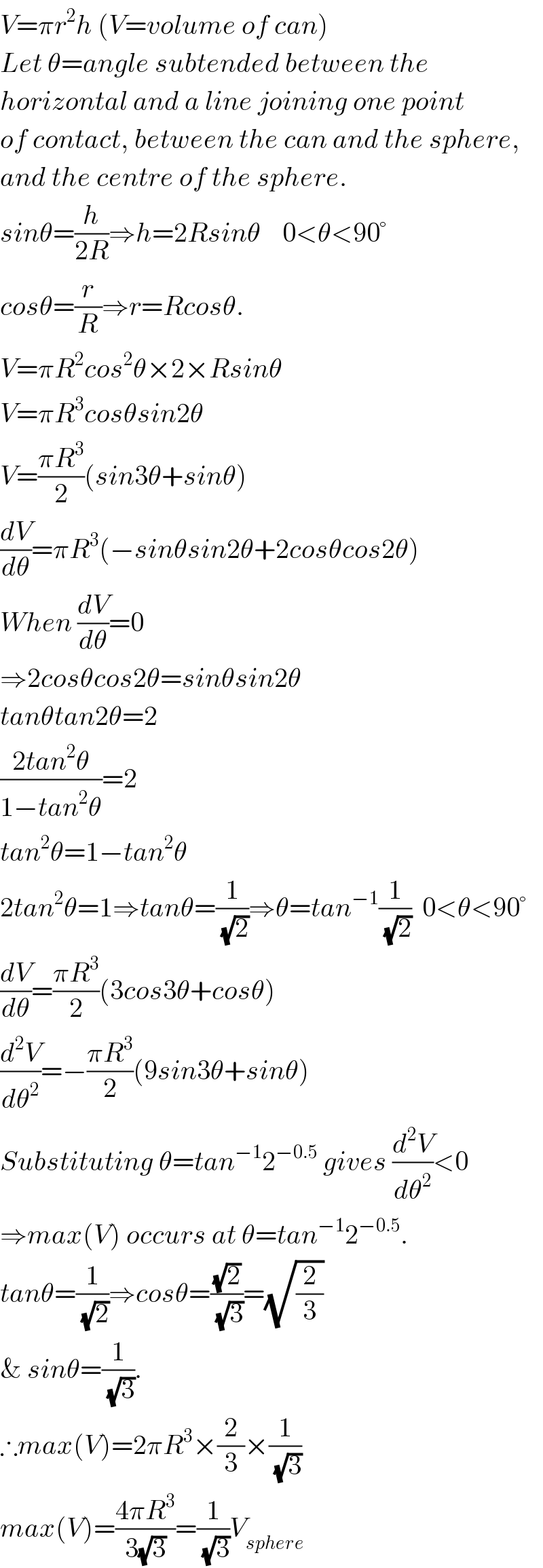
$${V}=\pi{r}^{\mathrm{2}} {h}\:\left({V}={volume}\:{of}\:{can}\right) \\ $$$${Let}\:\theta={angle}\:{subtended}\:{between}\:{the} \\ $$$${horizontal}\:{and}\:{a}\:{line}\:{joining}\:{one}\:{point} \\ $$$${of}\:{contact},\:{between}\:{the}\:{can}\:{and}\:{the}\:{sphere}, \\ $$$${and}\:{the}\:{centre}\:{of}\:{the}\:{sphere}. \\ $$$${sin}\theta=\frac{{h}}{\mathrm{2}{R}}\Rightarrow{h}=\mathrm{2}{Rsin}\theta\:\:\:\:\mathrm{0}<\theta<\mathrm{90}° \\ $$$${cos}\theta=\frac{{r}}{{R}}\Rightarrow{r}={Rcos}\theta. \\ $$$${V}=\pi{R}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta×\mathrm{2}×{Rsin}\theta \\ $$$${V}=\pi{R}^{\mathrm{3}} {cos}\theta{sin}\mathrm{2}\theta \\ $$$${V}=\frac{\pi{R}^{\mathrm{3}} }{\mathrm{2}}\left({sin}\mathrm{3}\theta+{sin}\theta\right) \\ $$$$\frac{{dV}}{{d}\theta}=\pi{R}^{\mathrm{3}} \left(−{sin}\theta{sin}\mathrm{2}\theta+\mathrm{2}{cos}\theta{cos}\mathrm{2}\theta\right) \\ $$$${When}\:\frac{{dV}}{{d}\theta}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{cos}\theta{cos}\mathrm{2}\theta={sin}\theta{sin}\mathrm{2}\theta \\ $$$${tan}\theta{tan}\mathrm{2}\theta=\mathrm{2} \\ $$$$\frac{\mathrm{2}{tan}^{\mathrm{2}} \theta}{\mathrm{1}−{tan}^{\mathrm{2}} \theta}=\mathrm{2} \\ $$$${tan}^{\mathrm{2}} \theta=\mathrm{1}−{tan}^{\mathrm{2}} \theta \\ $$$$\mathrm{2}{tan}^{\mathrm{2}} \theta=\mathrm{1}\Rightarrow{tan}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\Rightarrow\theta={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\mathrm{0}<\theta<\mathrm{90}° \\ $$$$\frac{{dV}}{{d}\theta}=\frac{\pi{R}^{\mathrm{3}} }{\mathrm{2}}\left(\mathrm{3}{cos}\mathrm{3}\theta+{cos}\theta\right) \\ $$$$\frac{{d}^{\mathrm{2}} {V}}{{d}\theta^{\mathrm{2}} }=−\frac{\pi{R}^{\mathrm{3}} }{\mathrm{2}}\left(\mathrm{9}{sin}\mathrm{3}\theta+{sin}\theta\right) \\ $$$${Substituting}\:\theta={tan}^{−\mathrm{1}} \mathrm{2}^{−\mathrm{0}.\mathrm{5}} \:{gives}\:\frac{{d}^{\mathrm{2}} {V}}{{d}\theta^{\mathrm{2}} }<\mathrm{0} \\ $$$$\Rightarrow{max}\left({V}\right)\:{occurs}\:{at}\:\theta={tan}^{−\mathrm{1}} \mathrm{2}^{−\mathrm{0}.\mathrm{5}} . \\ $$$${tan}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\Rightarrow{cos}\theta=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\&\:{sin}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}. \\ $$$$\therefore{max}\left({V}\right)=\mathrm{2}\pi{R}^{\mathrm{3}} ×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${max}\left({V}\right)=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{V}_{{sphere}} \\ $$
