Question Number 131852 by mnjuly1970 last updated on 09/Feb/21
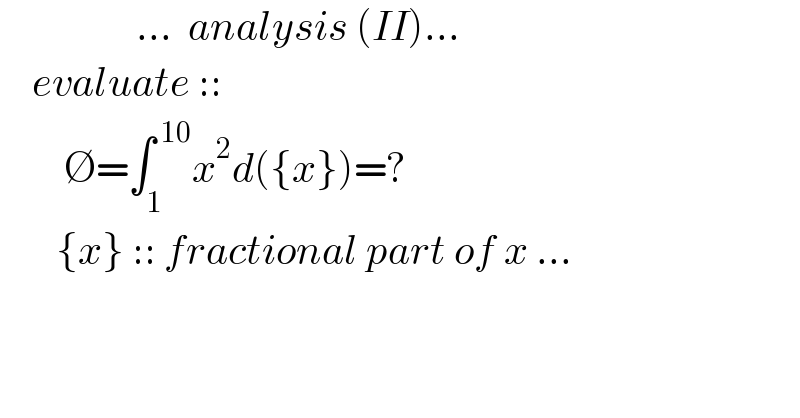
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\:{analysis}\:\left({II}\right)… \\ $$$$\:\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\varnothing=\int_{\mathrm{1}} ^{\:\mathrm{10}} {x}^{\mathrm{2}} {d}\left(\left\{{x}\right\}\right)=? \\ $$$$\:\:\:\:\:\:\:\left\{{x}\right\}\:::\:{fractional}\:{part}\:{of}\:{x}\:… \\ $$$$ \\ $$
Answered by mr W last updated on 09/Feb/21
![φ=∫_1 ^n x^2 d({x}) =Σ_(k=1) ^(n−1) ∫_k ^(k+1) x^2 d(x−k) =Σ_(k=1) ^(n−1) ∫_k ^(k+1) x^2 dx =(1/3)Σ_(k=1) ^(n−1) [(k+1)^3 −k^3 ] =(1/3)(n^3 −1) for n=10: φ=333](https://www.tinkutara.com/question/Q131859.png)
$$\phi=\int_{\mathrm{1}} ^{{n}} {x}^{\mathrm{2}} {d}\left(\left\{{x}\right\}\right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {x}^{\mathrm{2}} {d}\left({x}−{k}\right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {x}^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[\left({k}+\mathrm{1}\right)^{\mathrm{3}} −{k}^{\mathrm{3}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({n}^{\mathrm{3}} −\mathrm{1}\right) \\ $$$${for}\:{n}=\mathrm{10}: \\ $$$$\phi=\mathrm{333} \\ $$
Commented by mr W last updated on 09/Feb/21
$${where}\:{is}\:{the}\:{mistake}\:{sir}? \\ $$
