Question Number 9486 by Joel575 last updated on 10/Dec/16

$$\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{{n}}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{So},\:\frac{\mathrm{1}}{{n}}\:=\:? \\ $$
Answered by mrW last updated on 10/Dec/16

$$\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{{n}}\right)\:=\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}\:}\right) \\ $$$$\frac{\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{1}−\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\right)×\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{{n}}\right)\:}=\mathrm{1} \\ $$$$\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{7}}{\mathrm{11}} \\ $$$$\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{n}}\right)=\frac{\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{n}}}=\frac{\mathrm{5}+\mathrm{n}}{\mathrm{5n}−\mathrm{1}} \\ $$$$\frac{\frac{\mathrm{7}}{\mathrm{11}}+\frac{\mathrm{5}+\mathrm{n}}{\mathrm{5n}−\mathrm{1}}}{\mathrm{1}−\frac{\mathrm{7}}{\mathrm{11}}×\frac{\mathrm{5}+\mathrm{n}}{\mathrm{5n}−\mathrm{1}}}=\mathrm{1} \\ $$$$\mathrm{7}\left(\mathrm{5n}−\mathrm{1}\right)+\mathrm{11}\left(\mathrm{5}+\mathrm{n}\right)=\mathrm{11}\left(\mathrm{5n}−\mathrm{1}\right)−\mathrm{7}\left(\mathrm{5}+\mathrm{n}\right) \\ $$$$−\mathrm{20n}+\mathrm{4}+\mathrm{90}+\mathrm{18n}=\mathrm{0} \\ $$$$\mathrm{n}=\mathrm{47} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}=\frac{\mathrm{1}}{\mathrm{47}} \\ $$
Commented by Joel575 last updated on 11/Dec/16

$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by mrW last updated on 11/Dec/16
![arctan (1/n)=(π/4)−(arctan (1/3) + arctan (1/4) + arctan (1/5)) (1/n)=tan [(π/4)−(arctan (1/3) + arctan (1/4) + arctan (1/5))] (1/n)=((1−tan (arctan (1/3) + arctan (1/4) + arctan (1/5)))/(1+tan (arctan (1/3) + arctan (1/4) + arctan (1/5)))) tan (arctan (1/3) + arctan (1/4) + arctan (1/5)) =(((1/3)+tan (arctan (1/4) + arctan (1/5)))/(1−(1/3)tan (arctan (1/4) + arctan (1/5)))) =(((1/3)+(((1/4)+(1/5))/(1−(1/4)×(1/5))))/(1−(1/3)×(((1/4)+(1/5))/(1−(1/4)×(1/5)))))=(((1/3)+(9/(19)))/(1−(1/3)×(9/(19))))=((19+3×9)/(3×19−9))=((23)/(24)) ⇒(1/n)=((1−((23)/(24)))/(1+((23)/(24))))=((24−23)/(24+23))=(1/(47))](https://www.tinkutara.com/question/Q9504.png)
$$\mathrm{arctan}\:\frac{\mathrm{1}}{{n}}=\frac{\pi}{\mathrm{4}}−\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}=\mathrm{tan}\:\left[\frac{\pi}{\mathrm{4}}−\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right)\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}=\frac{\mathrm{1}−\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right)}{\mathrm{1}+\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right)} \\ $$$$ \\ $$$$\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:\left(\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{5}}\right)} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{5}}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{5}}}}=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{9}}{\mathrm{19}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{19}}}=\frac{\mathrm{19}+\mathrm{3}×\mathrm{9}}{\mathrm{3}×\mathrm{19}−\mathrm{9}}=\frac{\mathrm{23}}{\mathrm{24}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}=\frac{\mathrm{1}−\frac{\mathrm{23}}{\mathrm{24}}}{\mathrm{1}+\frac{\mathrm{23}}{\mathrm{24}}}=\frac{\mathrm{24}−\mathrm{23}}{\mathrm{24}+\mathrm{23}}=\frac{\mathrm{1}}{\mathrm{47}} \\ $$
Commented by Joel575 last updated on 11/Dec/16
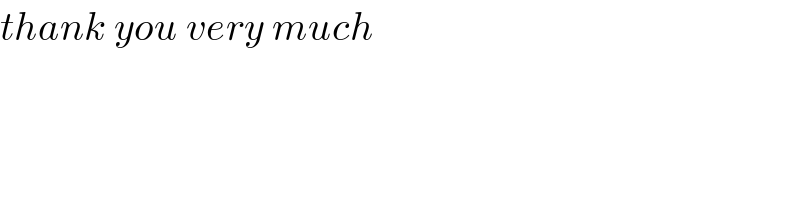
$${thank}\:{you}\:{very}\:{much} \\ $$
