Menu Close

arctan-x-1-dx-propose-par-Rodrigue-

Tinku Tara 0 Comments
Pin




Question Number 143167 by pticantor last updated on 10/Jun/21
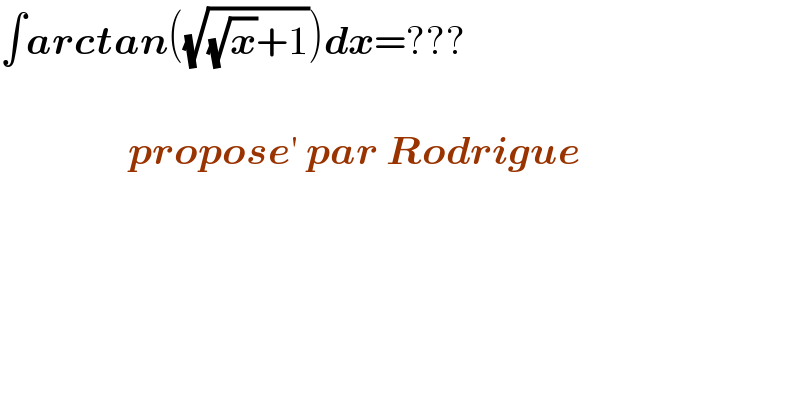
∫arctan((√((√x)+1)))dx=??? propose′ par Rodrigue
$$\int\boldsymbol{{arctan}}\left(\sqrt{\sqrt{\boldsymbol{{x}}}+\mathrm{1}}\right)\boldsymbol{{dx}}=??? \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{propose}}'\:\boldsymbol{{par}}\:\boldsymbol{{Rodrigue}} \\ $$
Answered by Olaf_Thorendsen last updated on 10/Jun/21
F(x) = ∫arctan((√((√x)+1)))dx F(x) = xarctan((√((√x)+1)))−∫x(((1/(2(√x)))/(2(√((√x)+1))))/(1+((√x)+1))) dx F(x) = xarctan((√((√x)+1)))−(1/4)∫((√x)/( ((√x)+2)(√((√x)+1)))) dx G(x) = ∫((√x)/( ((√x)+2)(√((√x)+1)))) dx Let u = (√x) G(u) = ∫(u/( (u+2)(√(u+1)))) 2udu G(u) = ∫((2u^2 )/( (u+2)(√(u+1)))) du Let v = (√(u+1)) G(v) = ∫((2(v^2 −1)^2 )/( (v^2 −1+2)v)) 2vdv G(v) = ∫((4(v^2 −1)^2 )/( v^2 +1)) dv G(v) = ∫[4v^2 −12+((16)/( v^2 +1))] dv G(v) = (4/3)v^3 −12v+16arctanv G(u) = (4/3)(u+1)^(3/2) −12(√(u+1))+16arctan((√(u+1))) G(x) = (4/3)((√x)+1)^(3/2) −12(√((√x)+1))+16arctan((√((√x)+1))) F(x) = xarctan((√((√x)+1)))−(1/4)G(x) F(x) = xarctan((√((√x)+1)))− (1/3)((√x)+1)^(3/2) +3(√((√x)+1))−4arctan((√((√x)+1))) F(x) = (x−4)arctan((√((√x)+1)))− (1/3)((√x)+1)^(3/2) +3(√((√x)+1))
$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right)−\int{x}\frac{\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{2}\sqrt{\sqrt{{x}}+\mathrm{1}}}}{\mathrm{1}+\left(\sqrt{{x}}+\mathrm{1}\right)}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\sqrt{{x}}}{\:\left(\sqrt{{x}}+\mathrm{2}\right)\sqrt{\sqrt{{x}}+\mathrm{1}}}\:{dx} \\ $$$$\mathrm{G}\left({x}\right)\:=\:\int\frac{\sqrt{{x}}}{\:\left(\sqrt{{x}}+\mathrm{2}\right)\sqrt{\sqrt{{x}}+\mathrm{1}}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\sqrt{{x}} \\ $$$$\mathrm{G}\left({u}\right)\:=\:\int\frac{{u}}{\:\left({u}+\mathrm{2}\right)\sqrt{{u}+\mathrm{1}}}\:\mathrm{2}{udu} \\ $$$$\mathrm{G}\left({u}\right)\:=\:\int\frac{\mathrm{2}{u}^{\mathrm{2}} }{\:\left({u}+\mathrm{2}\right)\sqrt{{u}+\mathrm{1}}}\:{du} \\ $$$$\mathrm{Let}\:{v}\:=\:\sqrt{{u}+\mathrm{1}} \\ $$$$\mathrm{G}\left({v}\right)\:=\:\int\frac{\mathrm{2}\left({v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\:\left({v}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}\right){v}}\:\mathrm{2}{vdv} \\ $$$$\mathrm{G}\left({v}\right)\:=\:\int\frac{\mathrm{4}\left({v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\:{v}^{\mathrm{2}} +\mathrm{1}}\:{dv} \\ $$$$\mathrm{G}\left({v}\right)\:=\:\int\left[\mathrm{4}{v}^{\mathrm{2}} −\mathrm{12}+\frac{\mathrm{16}}{\:{v}^{\mathrm{2}} +\mathrm{1}}\right]\:{dv} \\ $$$$\mathrm{G}\left({v}\right)\:=\:\frac{\mathrm{4}}{\mathrm{3}}{v}^{\mathrm{3}} −\mathrm{12}{v}+\mathrm{16arctan}{v} \\ $$$$\mathrm{G}\left({u}\right)\:=\:\frac{\mathrm{4}}{\mathrm{3}}\left({u}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} −\mathrm{12}\sqrt{{u}+\mathrm{1}}+\mathrm{16arctan}\left(\sqrt{{u}+\mathrm{1}}\right) \\ $$$$\mathrm{G}\left({x}\right)\:=\:\frac{\mathrm{4}}{\mathrm{3}}\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} −\mathrm{12}\sqrt{\sqrt{{x}}+\mathrm{1}}+\mathrm{16arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{G}\left({x}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right)−\:\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \\ $$$$+\mathrm{3}\sqrt{\sqrt{{x}}+\mathrm{1}}−\mathrm{4arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\left({x}−\mathrm{4}\right)\mathrm{arctan}\left(\sqrt{\sqrt{{x}}+\mathrm{1}}\right)−\:\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} +\mathrm{3}\sqrt{\sqrt{{x}}+\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 11/Jun/21
Φ=∫ arctan((√((√x)+1)))dx changement (√((√x)+1))=t give(√x)+1=t^2 ⇒ (√x)=t^2 −1 ⇒x=(t^2 −1)^2 ⇒dx=2(2t)(t^2 −1)=4t(t^2 −1) ⇒ Φ=∫4t(t^2 −1) arctan(t)dt =4∫(t^3 −t)arctan(t)dt =_(by parts) 4{ ((t^4 /4)−(t^2 /2))arctant −∫((t^4 /4)−(t^2 /2))(dt/(1+t^2 )) =(t^4 −2t^2 )arctant−∫(t^4 −2t^2 )(dt/(1+t^2 )) but ∫ ((t^4 −2t^2 )/(t^2 +1))dt =∫ ((t^2 (t^2 +1)−3t^2 )/(t^2 +1))dt =∫ t^2 dt−3∫ ((t^2 +1−1)/(t^2 +1))dt =(t^3 /3)−3t+3arctant +c ⇒ Φ=(t^4 −2t^2 )arctant−(t^3 /3)+3t−3arctant +C =(((√x)+1)^2 −2((√x)+1)−3)arctan((√((√x)+1)))−(1/3)((√((√x)+1)))^3 +3((√((√x)+1))) +C
$$\Phi=\int\:\mathrm{arctan}\left(\sqrt{\sqrt{\mathrm{x}}+\mathrm{1}}\right)\mathrm{dx}\:\mathrm{changement}\:\sqrt{\sqrt{\mathrm{x}}+\mathrm{1}}=\mathrm{t}\:\mathrm{give}\sqrt{\mathrm{x}}+\mathrm{1}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{x}}=\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{x}=\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{dx}=\mathrm{2}\left(\mathrm{2t}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{4t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\Phi=\int\mathrm{4t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\:\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{4}\int\left(\mathrm{t}^{\mathrm{3}} −\mathrm{t}\right)\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \mathrm{4}\left\{\:\:\left(\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\mathrm{arctant}\:−\int\left(\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right. \\ $$$$=\left(\mathrm{t}^{\mathrm{4}} −\mathrm{2t}^{\mathrm{2}} \right)\mathrm{arctant}−\int\left(\mathrm{t}^{\mathrm{4}} −\mathrm{2t}^{\mathrm{2}} \right)\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\:\:\mathrm{but} \\ $$$$\int\:\:\frac{\mathrm{t}^{\mathrm{4}} −\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\int\:\:\frac{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{3t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\int\:\mathrm{t}^{\mathrm{2}} \:\mathrm{dt}−\mathrm{3}\int\:\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{3t}+\mathrm{3arctant}\:+\mathrm{c}\:\Rightarrow \\ $$$$\Phi=\left(\mathrm{t}^{\mathrm{4}} −\mathrm{2t}^{\mathrm{2}} \right)\mathrm{arctant}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{3t}−\mathrm{3arctant}\:+\mathrm{C} \\ $$$$=\left(\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)−\mathrm{3}\right)\mathrm{arctan}\left(\sqrt{\sqrt{\mathrm{x}}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{\sqrt{\mathrm{x}}+\mathrm{1}}\right)^{\mathrm{3}} +\mathrm{3}\left(\sqrt{\sqrt{\mathrm{x}}+\mathrm{1}}\right)\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *