Question Number 651 by 123456 last updated on 19/Feb/15
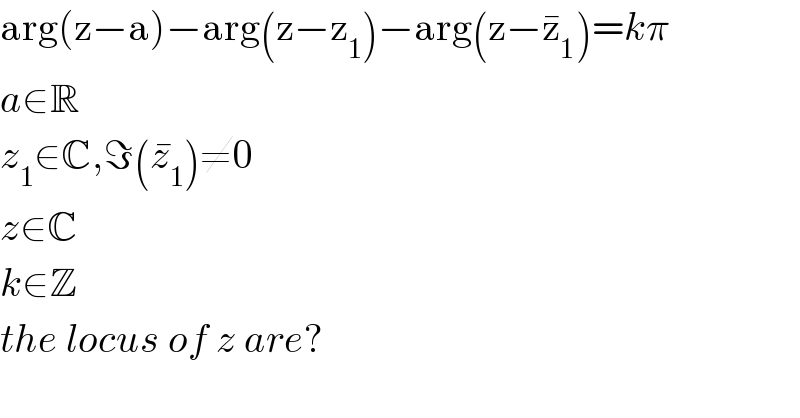
$$\mathrm{arg}\left(\mathrm{z}−\mathrm{a}\right)−\mathrm{arg}\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)−\mathrm{arg}\left(\mathrm{z}−\bar {\mathrm{z}}_{\mathrm{1}} \right)={k}\pi \\ $$$${a}\in\mathbb{R} \\ $$$${z}_{\mathrm{1}} \in\mathbb{C},\Im\left(\bar {{z}}_{\mathrm{1}} \right)\neq\mathrm{0} \\ $$$${z}\in\mathbb{C} \\ $$$${k}\in\mathbb{Z} \\ $$$${the}\:{locus}\:{of}\:{z}\:{are}? \\ $$
Commented by 123456 last updated on 20/Feb/15
![((z−a)/((z−z_1 )(z−z_1 ^� ))) =((z−a)/([z−(x_1 +y_1 ı)][z−(x_1 −y_1 ı)])) =((z−a)/([(z−x_1 )−y_1 ı][(z−x_1 )+y_1 ı])) =((z−a)/((z−x_1 )^2 −(y_1 ı)^2 )) =((z−a)/(z^2 −2zx_1 +x_1 ^2 +y_1 ^2 )) =((x+yı−a)/((x+yı)^2 −2(x+yı)x_1 +x_1 ^2 +y_1 ^2 )) =(((x−a)+yı)/(x^2 +2xyı−y^2 −2xx_1 −2yx_1 ı+x_1 ^2 +y_1 ^2 )) =(((x−a)+yı)/((x^2 +x_1 ^2 +y_1 ^2 −y^2 −2xx_1 )+(2xy−2yx_1 )ı)) =((u_1 +v_1 ı)/(u_2 +v_2 ı)) u_1 =x−a v_1 =y u_2 =x^2 +x_1 ^2 +y_1 ^2 −y^2 −2xx_1 v_2 =2xy−2yx_1 =(((u_1 +v_1 ı)(u_2 −v_2 ı))/((u_2 +v_2 ı)(u_2 −v_2 ı))) =((u_1 u_1 +v_1 v_2 )/(u_2 ^2 +v_2 ^2 ))+((−u_1 v_2 +v_1 u_2 )/(u_2 ^2 +v_2 ^2 ))ı −u_1 v_2 +v_1 u_2 =0 −(x−a)(2xy−2yx_1 )+y(x^2 +x_1 ^2 +y_1 ^2 −y^2 −2xx_1 )=0](https://www.tinkutara.com/question/Q664.png)
$$\frac{{z}−{a}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−\bar {{z}}_{\mathrm{1}} \right)} \\ $$$$=\frac{{z}−{a}}{\left[{z}−\left({x}_{\mathrm{1}} +{y}_{\mathrm{1}} \imath\right)\right]\left[{z}−\left({x}_{\mathrm{1}} −{y}_{\mathrm{1}} \imath\right)\right]} \\ $$$$=\frac{{z}−{a}}{\left[\left({z}−{x}_{\mathrm{1}} \right)−{y}_{\mathrm{1}} \imath\right]\left[\left({z}−{x}_{\mathrm{1}} \right)+{y}_{\mathrm{1}} \imath\right]} \\ $$$$=\frac{{z}−{a}}{\left({z}−{x}_{\mathrm{1}} \right)^{\mathrm{2}} −\left({y}_{\mathrm{1}} \imath\right)^{\mathrm{2}} } \\ $$$$=\frac{{z}−{a}}{{z}^{\mathrm{2}} −\mathrm{2}{zx}_{\mathrm{1}} +{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$=\frac{{x}+{y}\imath−{a}}{\left({x}+{y}\imath\right)^{\mathrm{2}} −\mathrm{2}\left({x}+{y}\imath\right){x}_{\mathrm{1}} +{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$=\frac{\left({x}−{a}\right)+{y}\imath}{{x}^{\mathrm{2}} +\mathrm{2}{xy}\imath−{y}^{\mathrm{2}} −\mathrm{2}{xx}_{\mathrm{1}} −\mathrm{2}{yx}_{\mathrm{1}} \imath+{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$=\frac{\left({x}−{a}\right)+{y}\imath}{\left({x}^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{xx}_{\mathrm{1}} \right)+\left(\mathrm{2}{xy}−\mathrm{2}{yx}_{\mathrm{1}} \right)\imath} \\ $$$$=\frac{{u}_{\mathrm{1}} +{v}_{\mathrm{1}} \imath}{{u}_{\mathrm{2}} +{v}_{\mathrm{2}} \imath} \\ $$$${u}_{\mathrm{1}} ={x}−{a} \\ $$$${v}_{\mathrm{1}} ={y} \\ $$$${u}_{\mathrm{2}} ={x}^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{xx}_{\mathrm{1}} \\ $$$${v}_{\mathrm{2}} =\mathrm{2}{xy}−\mathrm{2}{yx}_{\mathrm{1}} \\ $$$$=\frac{\left({u}_{\mathrm{1}} +{v}_{\mathrm{1}} \imath\right)\left({u}_{\mathrm{2}} −{v}_{\mathrm{2}} \imath\right)}{\left({u}_{\mathrm{2}} +{v}_{\mathrm{2}} \imath\right)\left({u}_{\mathrm{2}} −{v}_{\mathrm{2}} \imath\right)} \\ $$$$=\frac{{u}_{\mathrm{1}} {u}_{\mathrm{1}} +{v}_{\mathrm{1}} {v}_{\mathrm{2}} }{{u}_{\mathrm{2}} ^{\mathrm{2}} +{v}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{−{u}_{\mathrm{1}} {v}_{\mathrm{2}} +{v}_{\mathrm{1}} {u}_{\mathrm{2}} }{{u}_{\mathrm{2}} ^{\mathrm{2}} +{v}_{\mathrm{2}} ^{\mathrm{2}} }\imath \\ $$$$−{u}_{\mathrm{1}} {v}_{\mathrm{2}} +{v}_{\mathrm{1}} {u}_{\mathrm{2}} =\mathrm{0} \\ $$$$−\left({x}−{a}\right)\left(\mathrm{2}{xy}−\mathrm{2}{yx}_{\mathrm{1}} \right)+{y}\left({x}^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{xx}_{\mathrm{1}} \right)=\mathrm{0} \\ $$
