At-what-speed-should-a-basket-ball-player-project-a-ball-from-a-height-of-2-1-m-above-the-ground-at-an-angle-of-38-to-the-horizontal-so-that-it-just-passes-through-a-basket-ball-net-which-is-at-a-ho

FacebookTweetPin

Question Number 135618 by physicstutes last updated on 14/Mar/21

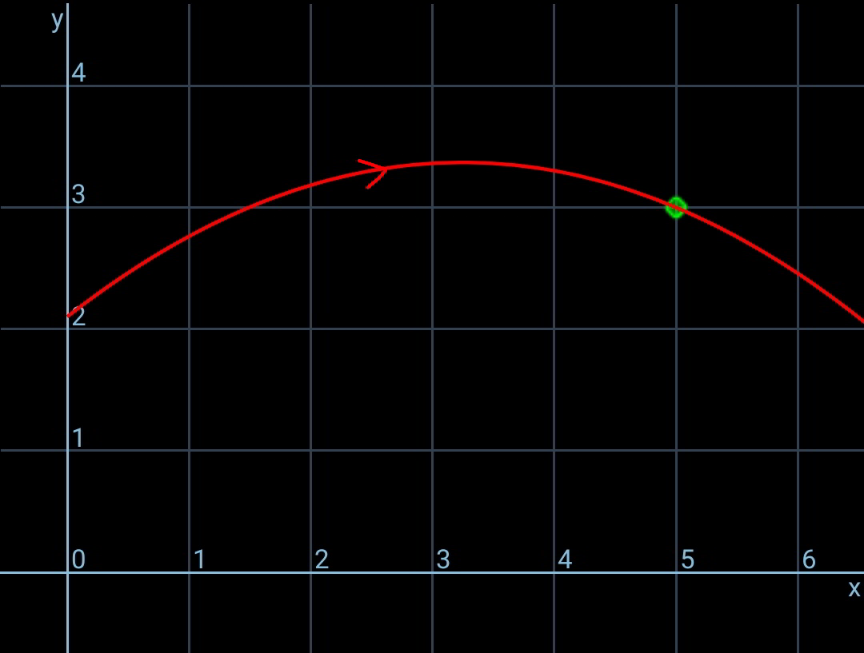
$$\mathrm{At}\mathrm{what}\mathrm{speed}\mathrm{should}\mathrm{a}\mathrm{basket}\mathrm{ball}\mathrm{player}\mathrm{project}\mathrm{a}\mathrm{ball}\mathrm{from}\mathrm{a}\mathrm{height}$$$$\mathrm{of}2.1\mathrm{m}$$$$\mathrm{above}\mathrm{the}\mathrm{ground}\mathrm{at}\mathrm{an}\mathrm{angle}\mathrm{of}38°$$$$\mathrm{to}\mathrm{the}\mathrm{horizontal}\mathrm{so}\mathrm{that}\mathrm{it}\mathrm{just}\mathrm{passes}\mathrm{through}\mathrm{a}\mathrm{basket}\mathrm{ball}\mathrm{net}\mathrm{which}$$$$\mathrm{is}\mathrm{at}\mathrm{a}\mathrm{horizontal}\mathrm{distance}\mathrm{of}5\mathrm{m}\mathrm{from}\mathrm{the}\mathrm{initial}$$$$\mathrm{position}\mathrm{of}\mathrm{the}\mathrm{ball}\mathrm{and}3\mathrm{m}\mathrm{above}\mathrm{the}\mathrm{playground}.\mathrm{at}\mathrm{determine}\mathrm{the}\mathrm{balls}$$$$\mathrm{maximum}\mathrm{height}\mathrm{above}\mathrm{the}\mathrm{ground}.$$

Answered by mr W last updated on 14/Mar/21

$$L=5m$$$$h=3-2.1=0.9m$$$$\theta =38°$$$$\frac{h}{L}=\tan \theta -\frac{gL}{2u^2}(1+{\tan }^2\theta )$$$$\Rightarrow u=\sqrt{\frac{gL(1+{\tan }^2\theta )}{2(\tan \theta -\frac{h}{L})}}\approx 8.18m/s$$$$h_{max}=\frac{u^2{\sin }^2\theta }{2g}=\frac{L(1+{\tan }^2\theta ){\sin }^2\theta }{4(\tan \theta -\frac{h}{L})}\approx 1.27m$$$$H_{max}=2.1+1.27=3.37maboveground$$

Commented by physicstutes last updated on 14/Mar/21

$$\mathrm{perfect}\mathrm{sir}$$

Commented by mr W last updated on 14/Mar/21

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin