Question Number 144025 by ZiYangLee last updated on 20/Jun/21
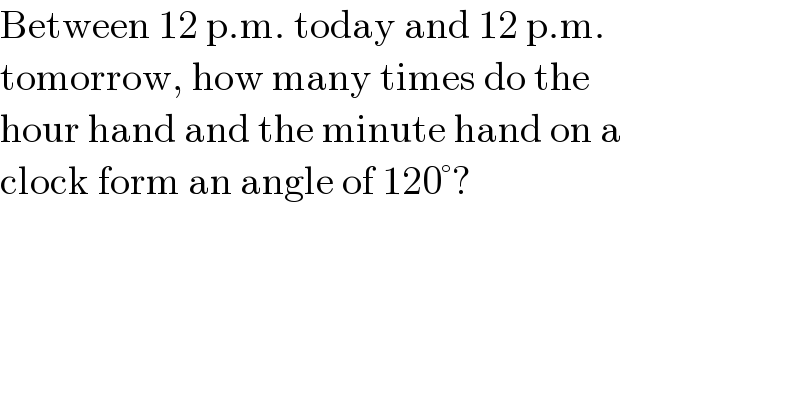
$$\mathrm{Between}\:\mathrm{12}\:\mathrm{p}.\mathrm{m}.\:\mathrm{today}\:\mathrm{and}\:\mathrm{12}\:\mathrm{p}.\mathrm{m}. \\ $$$$\mathrm{tomorrow},\:\mathrm{how}\:\mathrm{many}\:\mathrm{times}\:\mathrm{do}\:\mathrm{the} \\ $$$$\mathrm{hour}\:\mathrm{hand}\:\mathrm{and}\:\mathrm{the}\:\mathrm{minute}\:\mathrm{hand}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{clock}\:\mathrm{form}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{120}°? \\ $$
Answered by mr W last updated on 21/Jun/21
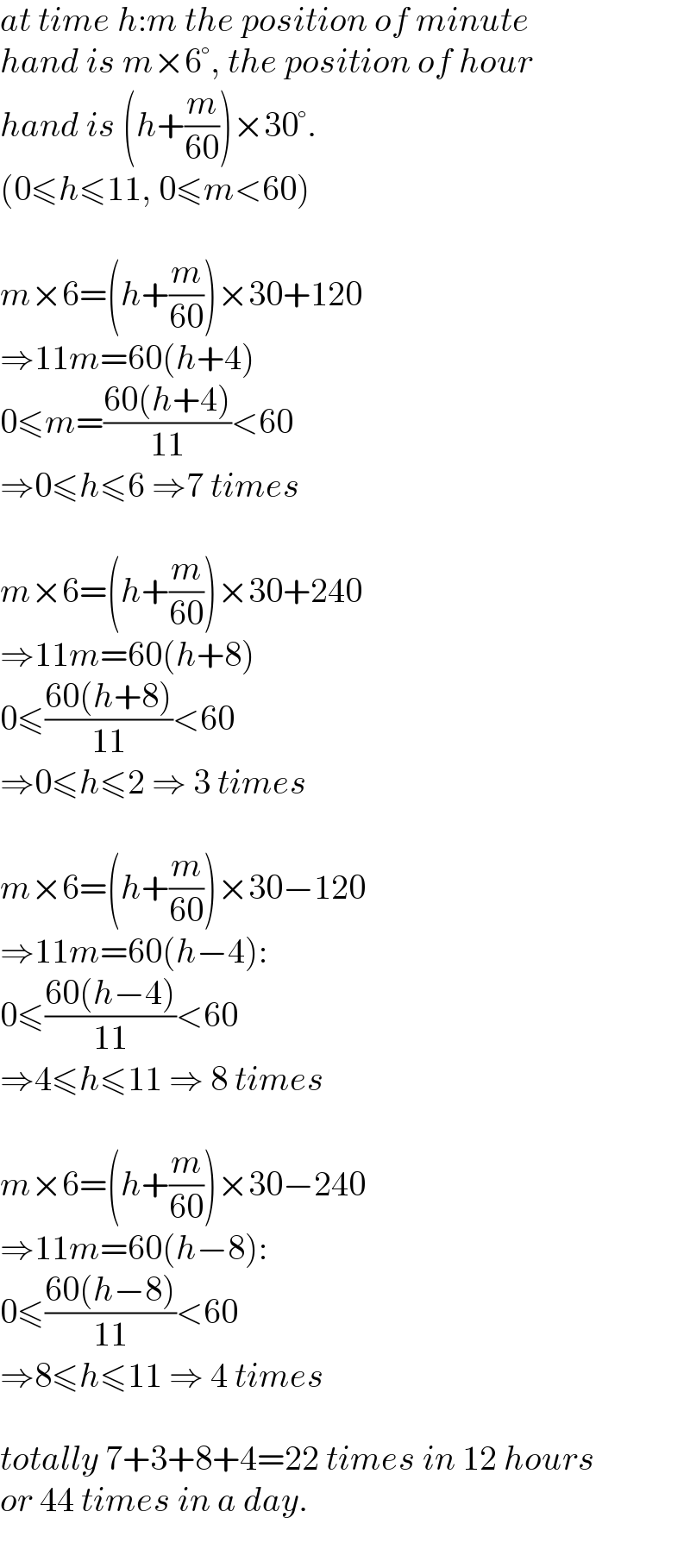
$${at}\:{time}\:{h}:{m}\:{the}\:{position}\:{of}\:{minute} \\ $$$${hand}\:{is}\:{m}×\mathrm{6}°,\:{the}\:{position}\:{of}\:{hour} \\ $$$${hand}\:{is}\:\left({h}+\frac{{m}}{\mathrm{60}}\right)×\mathrm{30}°. \\ $$$$\left(\mathrm{0}\leqslant{h}\leqslant\mathrm{11},\:\mathrm{0}\leqslant{m}<\mathrm{60}\right) \\ $$$$ \\ $$$${m}×\mathrm{6}=\left({h}+\frac{{m}}{\mathrm{60}}\right)×\mathrm{30}+\mathrm{120} \\ $$$$\Rightarrow\mathrm{11}{m}=\mathrm{60}\left({h}+\mathrm{4}\right) \\ $$$$\mathrm{0}\leqslant{m}=\frac{\mathrm{60}\left({h}+\mathrm{4}\right)}{\mathrm{11}}<\mathrm{60} \\ $$$$\Rightarrow\mathrm{0}\leqslant{h}\leqslant\mathrm{6}\:\Rightarrow\mathrm{7}\:{times} \\ $$$$ \\ $$$${m}×\mathrm{6}=\left({h}+\frac{{m}}{\mathrm{60}}\right)×\mathrm{30}+\mathrm{240} \\ $$$$\Rightarrow\mathrm{11}{m}=\mathrm{60}\left({h}+\mathrm{8}\right) \\ $$$$\mathrm{0}\leqslant\frac{\mathrm{60}\left({h}+\mathrm{8}\right)}{\mathrm{11}}<\mathrm{60} \\ $$$$\Rightarrow\mathrm{0}\leqslant{h}\leqslant\mathrm{2}\:\Rightarrow\:\mathrm{3}\:{times} \\ $$$$ \\ $$$${m}×\mathrm{6}=\left({h}+\frac{{m}}{\mathrm{60}}\right)×\mathrm{30}−\mathrm{120} \\ $$$$\Rightarrow\mathrm{11}{m}=\mathrm{60}\left({h}−\mathrm{4}\right): \\ $$$$\mathrm{0}\leqslant\frac{\mathrm{60}\left({h}−\mathrm{4}\right)}{\mathrm{11}}<\mathrm{60} \\ $$$$\Rightarrow\mathrm{4}\leqslant{h}\leqslant\mathrm{11}\:\Rightarrow\:\mathrm{8}\:{times} \\ $$$$ \\ $$$${m}×\mathrm{6}=\left({h}+\frac{{m}}{\mathrm{60}}\right)×\mathrm{30}−\mathrm{240} \\ $$$$\Rightarrow\mathrm{11}{m}=\mathrm{60}\left({h}−\mathrm{8}\right): \\ $$$$\mathrm{0}\leqslant\frac{\mathrm{60}\left({h}−\mathrm{8}\right)}{\mathrm{11}}<\mathrm{60} \\ $$$$\Rightarrow\mathrm{8}\leqslant{h}\leqslant\mathrm{11}\:\Rightarrow\:\mathrm{4}\:{times} \\ $$$$ \\ $$$${totally}\:\mathrm{7}+\mathrm{3}+\mathrm{8}+\mathrm{4}=\mathrm{22}\:{times}\:{in}\:\mathrm{12}\:{hours} \\ $$$${or}\:\mathrm{44}\:{times}\:{in}\:{a}\:{day}. \\ $$
