Question Number 4485 by Rasheed Soomro last updated on 31/Jan/16

$${By}\:\:{murging}\:\:{two}\:{sequences} \\ $$$$\:\:\:\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,…{a}_{{n}} \:\:\:{and}\:\:{b}_{\mathrm{1}} ,{b}_{\mathrm{2}} ,…,{b}_{{n}} \\ $$$${a}\:{new}\:{sequence}\: \\ $$$$\:\:\:\:{a}_{\mathrm{1}} ,{b}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{b}_{\mathrm{2}} ,…,{a}_{{n}} ,{b}_{{n}} \:\:{has}\:{been} \\ $$$${produced}. \\ $$$$\:\:\:\:\:\:{Determine}\:{a}\:\mathrm{single}-\mathrm{formula} \\ $$$$\mathrm{general}\:\mathrm{term}\:{of}\:{this}\:{new}\:{sequence} \\ $$$${in}\:{terms}\:{of}\:{a}_{{n}} \:{and}\:{b}_{{n}} \:. \\ $$
Commented by prakash jain last updated on 31/Jan/16
![c_n =(1/2)[a_n +(−1)^(n+1) a_n +b_n +(−1)^n b_n ]](https://www.tinkutara.com/question/Q4488.png)
$${c}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left[{a}_{{n}} +\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {a}_{{n}} +{b}_{{n}} +\left(−\mathrm{1}\right)^{{n}} {b}_{{n}} \right] \\ $$
Commented by FilupSmith last updated on 01/Feb/16
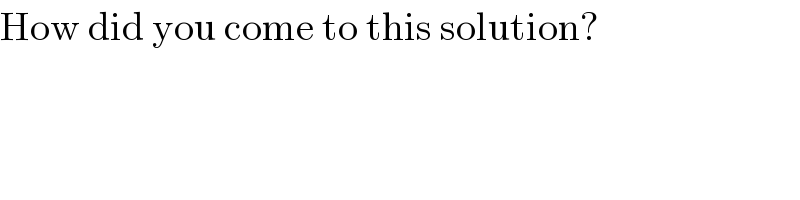
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{come}\:\mathrm{to}\:\mathrm{this}\:\mathrm{solution}? \\ $$
Commented by prakash jain last updated on 01/Feb/16
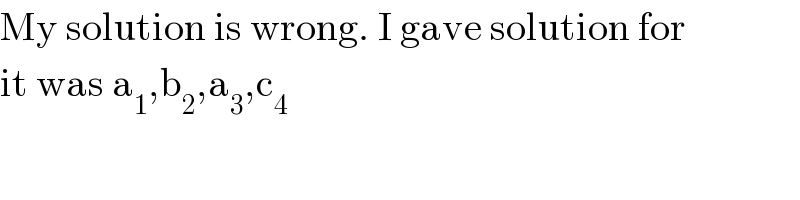
$$\mathrm{My}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{I}\:\mathrm{gave}\:\mathrm{solution}\:\mathrm{for} \\ $$$$\mathrm{it}\:\mathrm{was}\:\mathrm{a}_{\mathrm{1}} ,\mathrm{b}_{\mathrm{2}} ,\mathrm{a}_{\mathrm{3}} ,\mathrm{c}_{\mathrm{4}} \\ $$
Commented by Yozzii last updated on 01/Feb/16
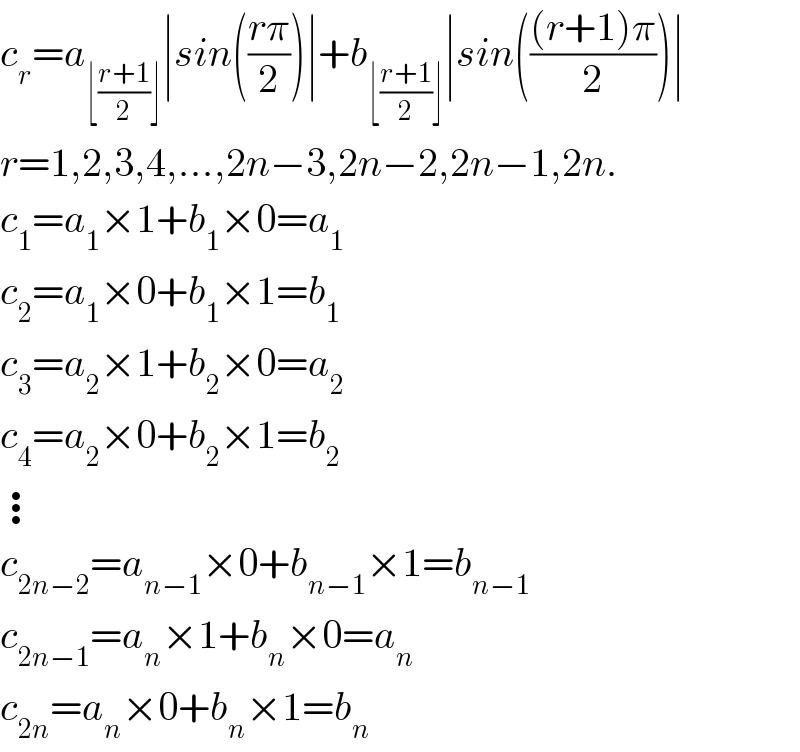
$${c}_{{r}} ={a}_{\lfloor\frac{{r}+\mathrm{1}}{\mathrm{2}}\rfloor} \mid{sin}\left(\frac{{r}\pi}{\mathrm{2}}\right)\mid+{b}_{\lfloor\frac{{r}+\mathrm{1}}{\mathrm{2}}\rfloor} \mid{sin}\left(\frac{\left({r}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)\mid \\ $$$${r}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},…,\mathrm{2}{n}−\mathrm{3},\mathrm{2}{n}−\mathrm{2},\mathrm{2}{n}−\mathrm{1},\mathrm{2}{n}. \\ $$$${c}_{\mathrm{1}} ={a}_{\mathrm{1}} ×\mathrm{1}+{b}_{\mathrm{1}} ×\mathrm{0}={a}_{\mathrm{1}} \\ $$$${c}_{\mathrm{2}} ={a}_{\mathrm{1}} ×\mathrm{0}+{b}_{\mathrm{1}} ×\mathrm{1}={b}_{\mathrm{1}} \\ $$$${c}_{\mathrm{3}} ={a}_{\mathrm{2}} ×\mathrm{1}+{b}_{\mathrm{2}} ×\mathrm{0}={a}_{\mathrm{2}} \\ $$$${c}_{\mathrm{4}} ={a}_{\mathrm{2}} ×\mathrm{0}+{b}_{\mathrm{2}} ×\mathrm{1}={b}_{\mathrm{2}} \\ $$$$\vdots \\ $$$${c}_{\mathrm{2}{n}−\mathrm{2}} ={a}_{{n}−\mathrm{1}} ×\mathrm{0}+{b}_{{n}−\mathrm{1}} ×\mathrm{1}={b}_{{n}−\mathrm{1}} \\ $$$${c}_{\mathrm{2}{n}−\mathrm{1}} ={a}_{{n}} ×\mathrm{1}+{b}_{{n}} ×\mathrm{0}={a}_{{n}} \\ $$$${c}_{\mathrm{2}{n}} ={a}_{{n}} ×\mathrm{0}+{b}_{{n}} ×\mathrm{1}={b}_{{n}} \\ $$
