Question Number 74885 by abdomathmax last updated on 03/Dec/19
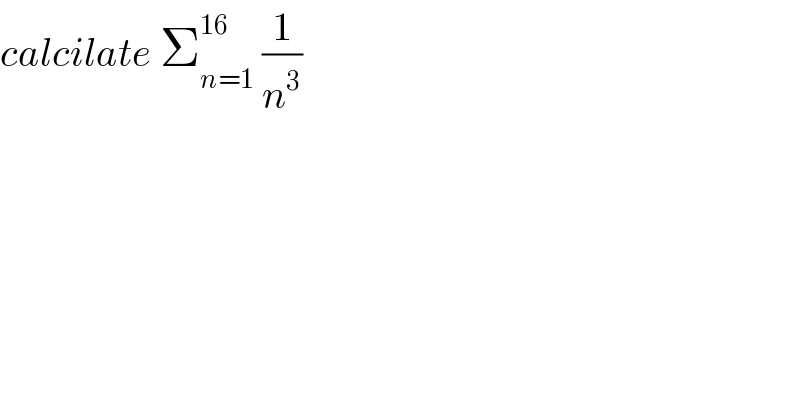
$${calcilate}\:\sum_{{n}=\mathrm{1}} ^{\mathrm{16}} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$
Answered by tw000001 last updated on 05/Dec/19

$$\mathrm{I}\:\mathrm{use}\:\mathrm{integral}\:\mathrm{to}\:\mathrm{solve}. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{16}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }=\int_{\mathrm{16}} ^{\mathrm{17}} \underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }{dn} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{17}} \underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }{dn}−\int_{\mathrm{1}} ^{\mathrm{16}} \underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }{dn}\approx\mathrm{1}.\mathrm{2002} \\ $$
