Question Number 138277 by mathmax by abdo last updated on 11/Apr/21
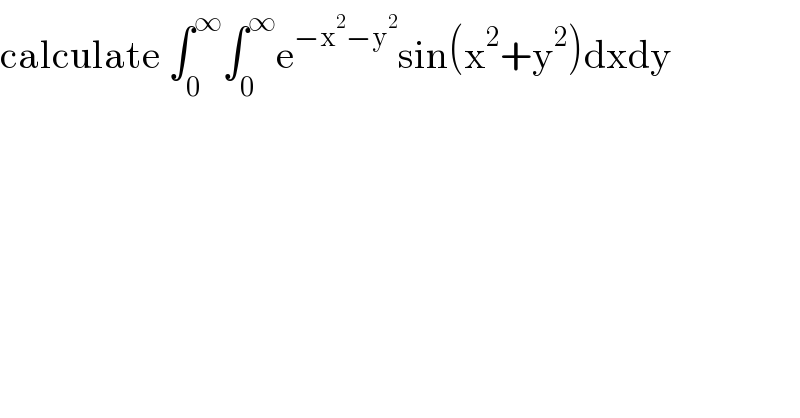
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\mathrm{dxdy} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Apr/21
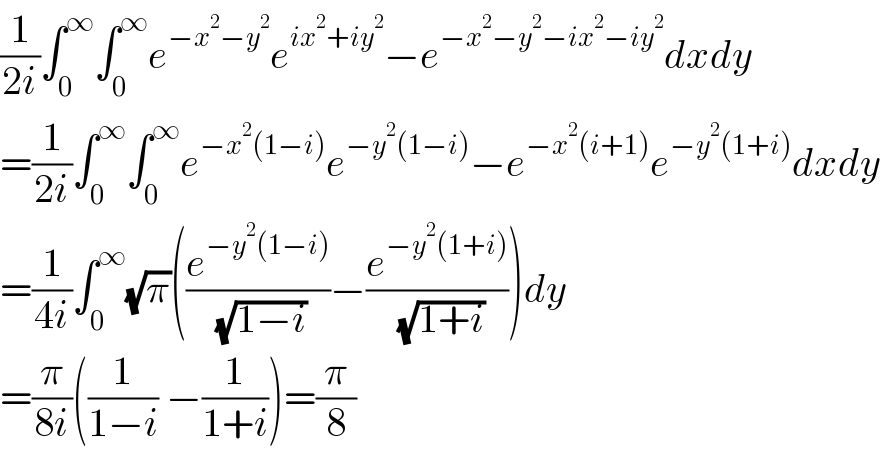
$$\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {e}^{{ix}^{\mathrm{2}} +{iy}^{\mathrm{2}} } −{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{ix}^{\mathrm{2}} −{iy}^{\mathrm{2}} } {dxdy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} \left(\mathrm{1}−{i}\right)} {e}^{−{y}^{\mathrm{2}} \left(\mathrm{1}−{i}\right)} −{e}^{−{x}^{\mathrm{2}} \left({i}+\mathrm{1}\right)} {e}^{−{y}^{\mathrm{2}} \left(\mathrm{1}+{i}\right)} {dxdy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\int_{\mathrm{0}} ^{\infty} \sqrt{\pi}\left(\frac{{e}^{−{y}^{\mathrm{2}} \left(\mathrm{1}−{i}\right)} }{\:\sqrt{\mathrm{1}−{i}}}−\frac{{e}^{−{y}^{\mathrm{2}} \left(\mathrm{1}+{i}\right)} }{\:\sqrt{\mathrm{1}+{i}}}\right){dy} \\ $$$$=\frac{\pi}{\mathrm{8}{i}}\left(\frac{\mathrm{1}}{\mathrm{1}−{i}}\:−\frac{\mathrm{1}}{\mathrm{1}+{i}}\right)=\frac{\pi}{\mathrm{8}}\:\: \\ $$
Answered by mnjuly1970 last updated on 11/Apr/21
![{_(y=rsin(θ)) ^(x:=rcos(θ)) J(r,θ)=((∂(x,y))/(∂(r,θ))) 𝛀=_(system) ^(polar) ∫_0 ^( (π/2)) ∫_0 ^( ∞) e^(−r^2 ) sin(r^2 )rdrdθ =^(r^2 =y) (1/2)∫_0 ^( (π/2)) ∫_0 ^( ∞) e^(−y) sin(y)dydθ =(1/2)∫_0 ^(π/2) ∫L [sin(y)]_(s=1) dθ =(1/2)∫_0 ^( (π/2)) (1/(1+1^2 ))dθ=(1/4).((π/2))=(π/8)...](https://www.tinkutara.com/question/Q138288.png)
$$\:\:\left\{_{{y}={rsin}\left(\theta\right)} ^{{x}:={rcos}\left(\theta\right)} \:\:\:\:{J}\left({r},\theta\right)=\frac{\partial\left({x},{y}\right)}{\partial\left({r},\theta\right)}\right. \\ $$$$\:\:\:\boldsymbol{\Omega}\underset{{system}} {\overset{{polar}} {=}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\:\infty} {e}^{−{r}^{\mathrm{2}} } {sin}\left({r}^{\mathrm{2}} \right){rdrd}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\overset{{r}^{\mathrm{2}} ={y}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\:\infty} {e}^{−{y}} {sin}\left({y}\right){dyd}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int\mathscr{L}\:\left[{sin}\left({y}\right)\right]_{{s}=\mathrm{1}} {d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}^{\mathrm{2}} }{d}\theta=\frac{\mathrm{1}}{\mathrm{4}}.\left(\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{8}}… \\ $$
Answered by mathmax by abdo last updated on 12/Apr/21
![Φ=∫_0 ^∞ ∫_0 ^∞ e^(−(x^2 +y^2 )) sin(x^2 +y^2 )dxdy we use the diffeomorphism { ((x=rcosθ⇒Φ=∫_0 ^∞ ∫_0 ^(π/2) e^(−r^2 ) sin(r^2 )rdrdθ)),((y=rsinθ)) :} Φ=(π/2)∫_0 ^∞ re^(−r^2 ) sin(r^2 )dr by parts ∫_0 ^∞ re^(−r^2 ) sin(r^2 )dr =[−(1/2)e^(−r^2 ) sin(r^2 )]_0 ^∞ +(1/2)∫_0 ^∞ e^(−r^2 ) (2r)cos(r^2 )dx =∫_0 ^∞ re^(−r^2 ) cos(r^2 )dr =Re(∫_0 ^∞ re^(−r^2 +ir^2 ) dr) and ∫_0 ^∞ r e^((−1+i)r^2 ) dr =_((√(1−i))r=z) ∫_0 ^∞ (z/( (√(1−i))))e^(−z^2 ) (dz/( (√(1−i)))) =(1/(1−i))∫_0 ^∞ ze^(−z^2 ) dz =(1/(1−i))[−(1/2)e^(−z^2 ) ]_0 ^∞ =(1/(2(1−i))) =((1+i)/4) ⇒∫_0 ^∞ re^(−r^2 ) cos(r^2 )dr=(1/4) ⇒Φ=(π/2).(1/4) ⇒Φ=(π/8)](https://www.tinkutara.com/question/Q138292.png)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)} \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\mathrm{dxdy}\:\:\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{diffeomorphism} \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{sin}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{rdrd}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases} \\ $$$$\Phi=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{sin}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}\:\:\mathrm{by}\:\mathrm{parts}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{sin}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} \:} \mathrm{sin}\left(\mathrm{r}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \left(\mathrm{2r}\right)\mathrm{cos}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{cos}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}\:\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{re}^{−\mathrm{r}^{\mathrm{2}} +\mathrm{ir}^{\mathrm{2}} } \mathrm{dr}\right)\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{r}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{r}^{\mathrm{2}} } \mathrm{dr}\:\:=_{\sqrt{\mathrm{1}−\mathrm{i}}\mathrm{r}=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}}{\:\sqrt{\mathrm{1}−\mathrm{i}}}\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \:\frac{\mathrm{dz}}{\:\sqrt{\mathrm{1}−\mathrm{i}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{i}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{ze}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{i}}\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{i}\right)} \\ $$$$=\frac{\mathrm{1}+\mathrm{i}}{\mathrm{4}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{cos}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\Phi=\frac{\pi}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\Phi=\frac{\pi}{\mathrm{8}} \\ $$
