Menu Close

calculate-0-1-e-2t-ln-1-t-dt-

Tinku Tara
Pin




Question Number 65925 by mathmax by abdo last updated on 05/Aug/19
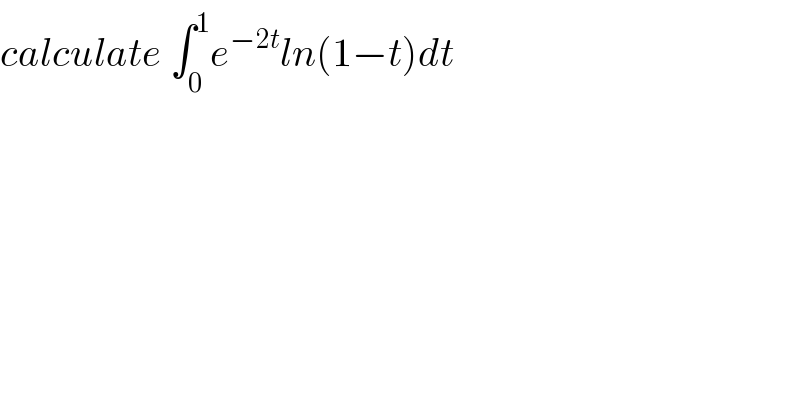
calculate ∫_0 ^1 e^(−2t) ln(1−t)dt
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right){dt} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
let I =∫_0 ^1 e^(−2t) ln(1−t)dt we have ln^′ (1−t) =((−1)/(1−t))=−Σ_(n=0) ^∞ t^n for ∣t∣<1 ⇒ln(1−t) =−Σ_(n=0) ^∞ (t^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (t^n /n) ⇒ I =−∫_0 ^1 e^(−2t) (Σ_(n=1) ^∞ (t^n /n))dt =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 t^n e^(−2t) dt let A_n =∫_0 ^1 t^n e^(−2t) dt by psrts u^′ =t^n and v=e^(−2t) A_n =[(1/(n+1))t^(n+1) e^(−2t) ]_0 ^1 −∫_0 ^1 (t^(n+1) /(n+1))(−2)e^(−2t) dt =(e^(−2) /(n+1)) +(2/(n+1)) ∫_0 ^1 t^(n+1) e^(−2t) dt⇒(n+1)A_n =e^(−2) +2A_(n+1) ⇒ 2A_(n+1) =(n+1)A_n −e^(−2) ⇒A_(n+1) =(((n+1))/2)A_n −(e^(−2) /2) ⇒ A_n =(n/2)A_(n−1) −(e^(−2) /2) let V_n =2(A_n /(n!)) ⇒ V_(n+1) −V_n =2(A_(n+1) /((n+1)!))−2(A_n /(n!)) =2(((n+1)A_n )/(2(n+1)!))−2(e^(−2) /2)−2(A_n /(n!)) =(A_n /(n!))−2(A_n /(n!)) −e^(−2) =−(1/(n!))A_n −e^(−2) ⇒Σ_(k=0) ^(n−1) (V_(k+1) −V_k ) =−Σ_(k=0) ^(n−1) (A_k /(k!))−ne^(−2) ⇒V_n −V_0 =−Σ_(k=0) ^(n−1) (A_k /(k!)) −ne^(−2) ⇒ V_n =V_0 −ne^(−2) −Σ_(k=0) ^(n−1) (A_k /(k!)) ...be continued...
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right){dt}\:\:{we}\:{have}\:\:{ln}^{'} \left(\mathrm{1}−{t}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−{t}}=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{{n}} \: \\ $$$${for}\:\mid{t}\mid<\mathrm{1}\:\Rightarrow{ln}\left(\mathrm{1}−{t}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\:\Rightarrow \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\right){dt}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} {e}^{−\mathrm{2}{t}} {dt} \\ $$$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \:{e}^{−\mathrm{2}{t}} {dt}\:\:\:{by}\:{psrts}\:{u}^{'} \:={t}^{{n}} \:{and}\:{v}={e}^{−\mathrm{2}{t}} \\ $$$${A}_{{n}} =\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} {e}^{−\mathrm{2}{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\left(−\mathrm{2}\right){e}^{−\mathrm{2}{t}} \:{dt} \\ $$$$=\frac{{e}^{−\mathrm{2}} }{{n}+\mathrm{1}}\:+\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}+\mathrm{1}} {e}^{−\mathrm{2}{t}} \:{dt}\Rightarrow\left({n}+\mathrm{1}\right){A}_{{n}} ={e}^{−\mathrm{2}} +\mathrm{2}{A}_{{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{2}{A}_{{n}+\mathrm{1}} =\left({n}+\mathrm{1}\right){A}_{{n}} −{e}^{−\mathrm{2}} \:\Rightarrow{A}_{{n}+\mathrm{1}} =\frac{\left({n}+\mathrm{1}\right)}{\mathrm{2}}{A}_{{n}} −\frac{{e}^{−\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{{n}}{\mathrm{2}}{A}_{{n}−\mathrm{1}} −\frac{{e}^{−\mathrm{2}} }{\mathrm{2}}\:\:\:{let}\:\:{V}_{{n}} =\mathrm{2}\frac{{A}_{{n}} }{{n}!}\:\Rightarrow \\ $$$${V}_{{n}+\mathrm{1}} −{V}_{{n}} =\mathrm{2}\frac{{A}_{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}−\mathrm{2}\frac{{A}_{{n}} }{{n}!}\:=\mathrm{2}\frac{\left({n}+\mathrm{1}\right){A}_{{n}} }{\mathrm{2}\left({n}+\mathrm{1}\right)!}−\mathrm{2}\frac{{e}^{−\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\frac{{A}_{{n}} }{{n}!} \\ $$$$=\frac{{A}_{{n}} }{{n}!}−\mathrm{2}\frac{{A}_{{n}} }{{n}!}\:−{e}^{−\mathrm{2}} \:=−\frac{\mathrm{1}}{{n}!}{A}_{{n}} −{e}^{−\mathrm{2}} \:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({V}_{{k}+\mathrm{1}} −{V}_{{k}} \right) \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \frac{{A}_{{k}} }{{k}!}−{ne}^{−\mathrm{2}} \:\:\Rightarrow{V}_{{n}} −{V}_{\mathrm{0}} =−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{A}_{{k}} }{{k}!}\:−{ne}^{−\mathrm{2}} \:\Rightarrow \\ $$$${V}_{{n}} ={V}_{\mathrm{0}} −{ne}^{−\mathrm{2}} −\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{A}_{{k}} }{{k}!}\:\:…{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
at form of serie we have e^(−2t) =Σ_(n=0) ^∞ (((−2t)^n )/(n!)) and ln(1−t) =−Σ_(n=1) ^∞ (t^n /n) ⇒e^(−2t) ln(1−t) =−(Σ_(n=0) ^∞ (((−2)^n t^n )/(n!)))(Σ_(n=1) ^∞ (t^n /n)) =−(1+Σ_(n=1) ^∞ (((−2)^n t^n )/(n!)))Σ_(n=1) ^∞ (t^n /n) =−Σ_(n=1) ^∞ (t^n /n) −(Σ_(n=1) ^∞ (((−2)^n t^n )/(n!)))(Σ_(n=1) ^∞ (t^n /n)) =ln(1−t)−Σ_(n=1) ^∞ c_n t^n with c_n =Σ_(i+j=1) a_i b_j =Σ_(i=1) ^(n−1) a_i b_(n−i) =Σ_(i=1) ^(n−1) (((−2)^i )/(i!))(1/(n−i)) ⇒ e^(−2t) ln(1−t) =ln(1−t)−Σ_(n=1) ^∞ (Σ_(i=1) ^(n−1) (((−2)^i )/((n−i)i!)))t^n ⇒ ∫_0 ^1 e^(−2t) ln(1−t)dt =∫_0 ^1 ln(1−t)dt −Σ_(n=1) ^∞ (Σ_(i=1) ^(n−1) (((−2)^i )/((n−i)i!)))(1/(n+1)) ∫_0 ^1 ln(1−t)dt =_(1−t =u) −∫_0 ^1 ln(u)(−du) =∫_0 ^1 ln(u)du =[ulnu−u]_0 ^1 =−1 ⇒ ∫_0 ^1 ln(1−t)dt =−1−Σ_(n=1) ^∞ (1/(n+1))(Σ_(i=1) ^(n−1) (((−2)^i )/((n−i)i!)))
$${at}\:{form}\:{of}\:{serie}\:\:{we}\:{have}\:{e}^{−\mathrm{2}{t}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}{t}\right)^{{n}} }{{n}!} \\ $$$${and}\:{ln}\left(\mathrm{1}−{t}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\:\Rightarrow{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right) \\ $$$$=−\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} {t}^{{n}} }{{n}!}\right)\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\right)\:=−\left(\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} {t}^{{n}} }{{n}!}\right)\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\:−\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} {t}^{{n}} }{{n}!}\right)\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\right) \\ $$$$={ln}\left(\mathrm{1}−{t}\right)−\sum_{{n}=\mathrm{1}} ^{\infty} \:{c}_{{n}} {t}^{{n}} \:\:\:\:{with}\:{c}_{{n}} =\sum_{{i}+{j}=\mathrm{1}} {a}_{{i}} {b}_{{j}} \:=\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} {a}_{{i}} {b}_{{n}−{i}} \\ $$$$=\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{2}\right)^{{i}} }{{i}!}\frac{\mathrm{1}}{{n}−{i}}\:\Rightarrow \\ $$$${e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right)\:={ln}\left(\mathrm{1}−{t}\right)−\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{2}\right)^{{i}} }{\left({n}−{i}\right){i}!}\right){t}^{{n}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right){dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}\right){dt}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \frac{\left(−\mathrm{2}\right)^{{i}} }{\left({n}−{i}\right){i}!}\right)\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}\right){dt}\:=_{\mathrm{1}−{t}\:={u}} \:\:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({u}\right)\left(−{du}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({u}\right){du} \\ $$$$=\left[{ulnu}−{u}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}\right){dt}\:=−\mathrm{1}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{2}\right)^{{i}} }{\left({n}−{i}\right){i}!}\right) \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
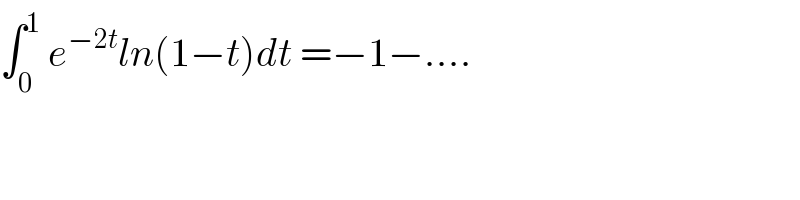
∫_0 ^1 e^(−2t) ln(1−t)dt =−1−....
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{t}\right){dt}\:=−\mathrm{1}−…. \\ $$

Pin