Menu Close

calculate-0-4pi-d-x-2-2x-cos-1-2-

Tinku Tara 0 Comments
Pin




Question Number 141222 by mathmax by abdo last updated on 16/May/21
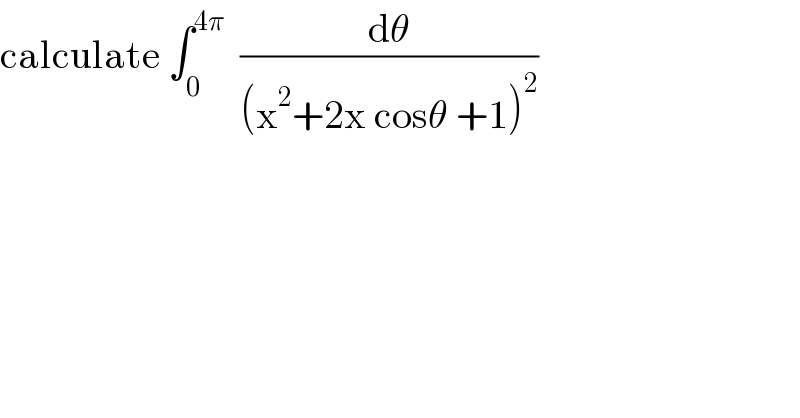
calculate ∫_0 ^(4π) (dθ/((x^2 +2x cosθ +1)^2 ))
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\:\frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\:\mathrm{cos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 16/May/21
Ω=∫_0 ^(4π) (dθ/((x^2 +2xcosθ+1)^2 ))=4∫_0 ^π (dθ/((x^2 +2xcosθ+1)^2 )), t=tan(θ/2) =4∫_0 ^∞ ((2dt)/((x^2 +2x∙((1−t^2 )/(1+t^2 ))+1)^2 ))∙(1/(1+t^2 )) =8∫_0 ^∞ ((t^2 +1)/((x^2 (1+t^2 )+2x(1−t^2 )+1+t^2 )^2 ))dt =8∫_0 ^∞ ((t^2 +1)/(((x^2 −2x+1)t^2 +(x^2 +2x+1))^2 ))dt =8∫_0 ^∞ ((t^2 +1)/(((x−1)^2 t^2 +(x+1)^2 )^2 ))=(8/((x−1)^4 ))∫_0 ^∞ ((t^2 +1)/((t^2 +(((x+1)/(x−1)))^2 )^2 )) =(8/((x−1)^4 )){∫_0 ^∞ ((t^2 +(((x+1)/(x−1)))^2 )/((t^2 +(((x+1)/(x−1)))^2 )^2 ))dt+∫_0 ^∞ ((1−(((x+1)/(x−1)))^2 )/((t^2 +(((x+1)/(x−1)))^2 )^2 ))dt} f(a)=∫_0 ^∞ (dt/(t^2 +a^2 ))=(π/(2a))⇒f ′(a)=−∫_0 ^∞ ((2a)/((t^2 +a^2 )^2 ))dt=−(π/(2a^2 )) ⇒∫_0 ^∞ (dt/((t^2 +a^2 )^2 ))=(π/(4a^3 )) Ω=(8/((x−1)^4 )){(π/(2(((x+1)/(x−1)))))+(1−(((x+1)/(x−1)))^2 )×(π/(4(((x+1)/(x−1)))^3 ))}
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2xcos}\theta+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{4}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2xcos}\theta+\mathrm{1}\right)^{\mathrm{2}} },\:\mathrm{t}=\mathrm{tan}\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2dt}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\centerdot\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)+\mathrm{2x}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)+\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)\mathrm{t}^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{8}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} +\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\mathrm{8}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }\left\{\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} +\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} +\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\right\} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2a}}\Rightarrow\mathrm{f}\:'\left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2a}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}=−\frac{\pi}{\mathrm{2a}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\pi}{\mathrm{4a}^{\mathrm{3}} } \\ $$$$\Omega=\frac{\mathrm{8}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }\left\{\frac{\pi}{\mathrm{2}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)}+\left(\mathrm{1}−\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \right)×\frac{\pi}{\mathrm{4}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{3}} }\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *