Menu Close

calculate-0-arctan-2x-x-2-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 74484 by mathmax by abdo last updated on 24/Nov/19
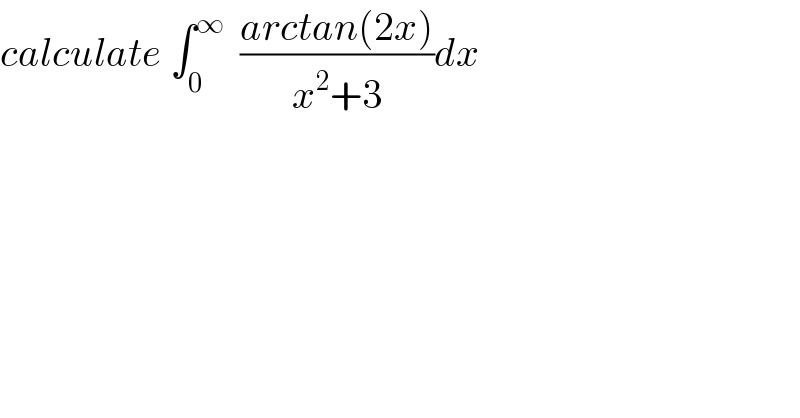
calculate ∫_0 ^∞ ((arctan(2x))/(x^2 +3))dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Nov/19
let f(t)=∫_0 ^∞ ((arctan(tx))/(x^2 +3))dx with t≥0 f^′ (t) =∫_0 ^∞ (x/((1+t^2 x^2 )(x^2 +3)))dx =_(tx=u) ∫_0 ^∞ (u/(t(1+u^2 )((u^2 /t^2 )+3)))(du/t) =∫_0 ^∞ ((udu)/((u^2 +1)(u^2 +3t^2 ))) decompsition of F(u)=(1/((u^2 +1)(u^2 +3t^2 ))) F(u)=((au+b)/(u^2 +1)) +((cu +d)/(u^2 +3t^2 )) F(−u)=F(u) ⇒((−au+b)/(u^2 +1)) +((−cu+d)/(u^2 +3t^2 )) =F(u) ⇒a=c=0 ⇒ F(u) =(b/(u^2 +1)) +(d/(u^2 +3t^2 )) lim_(u→+∞) u^2 F(u) =0 =b+d ⇒d=−b ⇒F(u)=(b/(u^2 +1))−(b/(u^2 +3t^2 )) F(0)=(1/(3t^2 )) =b−(b/(3t^2 )) =(((3t^2 −1)/(3t^2 )))b ⇒b=(1/(3t^2 −1)) ⇒ F(u) =(1/(3t^2 −1)){(1/(u^2 +1))−(1/(u^2 +3t^2 ))} ⇒ f^′ (t)=(1/(3t^2 −1)) ∫_0 ^∞ (du/(1+u^2 ))−(1/(3t^2 −1))∫_0 ^∞ (du/(u^2 +3t^2 )) ∫_0 ^∞ (du/(1+u^2 )) =(π/2) ∫_0 ^∞ (du/(u^2 +3t^2 )) =_(u=(√3)t z) ∫_0 ^∞ (((√3)t dz)/(3t^2 (1+z^2 ))) =(1/( (√3)t))×(π/2) ⇒ f^′ (t) =(π/(2(3t^2 −1)))−(π/(2(√3)t(3t^2 −1))) ⇒ f(t)=(π/2) ∫ (dt/(3t^2 −1))−(π/(2(√3))) ∫ (dt/(t(3t^2 −1))) +c ....be continued ....
$${let}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({tx}\right)}{{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}\:\:\:\:{with}\:{t}\geqslant\mathrm{0} \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}}{\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx}\:\:=_{{tx}={u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}}{{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\frac{{u}^{\mathrm{2}} }{{t}^{\mathrm{2}} }+\mathrm{3}\right)}\frac{{du}}{{t}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{udu}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{2}} \right)}\:{decompsition}\:{of}\:{F}\left({u}\right)=\frac{\mathrm{1}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{2}} \right)} \\ $$$${F}\left({u}\right)=\frac{{au}+{b}}{{u}^{\mathrm{2}} +\mathrm{1}}\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$${F}\left(−{u}\right)={F}\left({u}\right)\:\Rightarrow\frac{−{au}+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{cu}+{d}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} }\:={F}\left({u}\right)\:\Rightarrow{a}={c}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{{b}}{{u}^{\mathrm{2}} +\mathrm{1}}\:+\frac{{d}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {u}^{\mathrm{2}} {F}\left({u}\right)\:=\mathrm{0}\:={b}+{d}\:\Rightarrow{d}=−{b}\:\Rightarrow{F}\left({u}\right)=\frac{{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}−\frac{{b}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\:={b}−\frac{{b}}{\mathrm{3}{t}^{\mathrm{2}} }\:=\left(\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\right){b}\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}\left\{\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} }\:=_{{u}=\sqrt{\mathrm{3}}{t}\:{z}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{\mathrm{3}}{t}\:{dz}}{\mathrm{3}{t}^{\mathrm{2}} \left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}{t}}×\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\frac{\pi}{\mathrm{2}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}}\:\int\:\:\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\int\:\:\frac{{dt}}{{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}\:+{c}\:….{be}\:{continued}\:…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *