Menu Close

calculate-0-arctan-x-2-1-x-2-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 68038 by mathmax by abdo last updated on 03/Sep/19
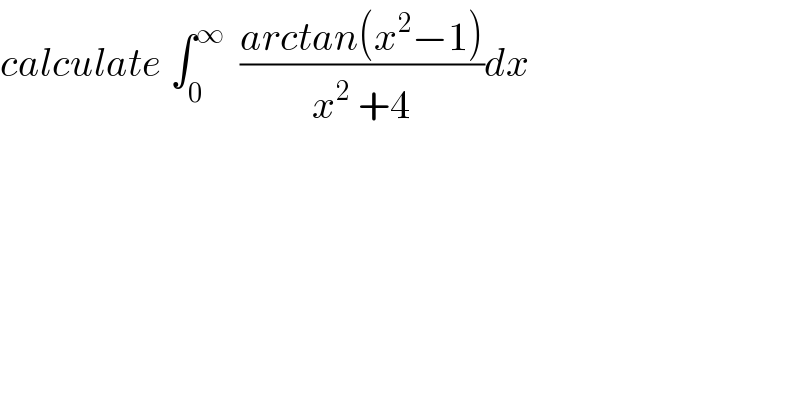
calculate ∫_0 ^∞ ((arctan(x^2 −1))/(x^2 +4))dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$
Commented by mathmax by abdo last updated on 07/Sep/19
let f(t) =∫_0 ^∞ ((arctan(x^2 −t))/(x^2 +4)) dx⇒f(1) =∫_0 ^∞ ((arctan(x^2 −1))/(x^2 +4))dx f^′ (t) =∫_0 ^∞ (1/((x^2 +4)(1+(x^2 −t)^2 )))dx =∫_0 ^∞ (dx/((x^2 +4)(x^4 −2tx^2 +t^2 +1))) ⇒2f^′ (t) =∫_(−∞) ^(+∞ ) (dx/((x^2 +4)(x^4 −2tx^(2 ) +t^2 +1))) let W(z) =(1/((z^2 +4)(z^4 −2tz^2 +t^(2 ) +1))) poles of W? z^2 +4 =0 ⇒z =+^− 2i z^4 −2tz^2 +t^2 +1 =0 ⇒u^2 −2tu +t^(2 ) +1 =0 with u=z^2 Δ^′ =t^2 −(t^2 +1) =−1 ⇒u_1 =t+i and u_2 =t−i ⇒ u_1 =(√(1+t^2 )) e^(iarctan((1/t))) and u_2 =(√(1+t^2 )) e^(−iarctan((1/t))) z^2 =u_1 ⇒z =+^− (1+t^2 )^(1/4) e^((i/2)arctan((1/t))) z^2 =u_2 ⇒z =+^− (1+t^2 )^(−(i/2)arctan((1/(t )))) ⇒ W(z) =(1/((z−2i)(z+2i)(z−(1+t^2 )^(1/4) e^((i/2)arctan((1/t))) (z+(1+t^2 )^(1/4) e^((i/2)arctan((1/t))) )(z−(1+t^2 )^(1/4) e^(−(i/2)arctan((1/t))) )(z+(1+t^2 )e^(−(i/2)arctan((1/t))) ))) residustheorem ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ{ Res(W,2i) +Res(W,(1+t^2 )^(1/4) e^((i/2)arctan((1/t))) +Res(W,−(1+t^2 )^(1/4) e^(−(i/2)afctan((1/t))) }...be continued...
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} −{t}\right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:{dx}\Rightarrow{f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{4}\right)\left(\mathrm{1}+\left({x}^{\mathrm{2}} −{t}\right)^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{4}\right)\left({x}^{\mathrm{4}} −\mathrm{2}{tx}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\mathrm{2}{f}^{'} \left({t}\right)\:=\int_{−\infty} ^{+\infty\:} \:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{4}\right)\left({x}^{\mathrm{4}} −\mathrm{2}{tx}^{\mathrm{2}\:} +{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${let}\:{W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)\left({z}^{\mathrm{4}} −\mathrm{2}{tz}^{\mathrm{2}} \:+{t}^{\mathrm{2}\:} +\mathrm{1}\right)}\:\:{poles}\:{of}\:{W}? \\ $$$${z}^{\mathrm{2}} \:+\mathrm{4}\:=\mathrm{0}\:\Rightarrow{z}\:=\overset{−} {+}\mathrm{2}{i} \\ $$$${z}^{\mathrm{4}} −\mathrm{2}{tz}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{u}^{\mathrm{2}} −\mathrm{2}{tu}\:+{t}^{\mathrm{2}\:} +\mathrm{1}\:=\mathrm{0}\:{with}\:{u}={z}^{\mathrm{2}} \\ $$$$\Delta^{'} ={t}^{\mathrm{2}} −\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:=−\mathrm{1}\:\Rightarrow{u}_{\mathrm{1}} ={t}+{i}\:\:{and}\:{u}_{\mathrm{2}} ={t}−{i}\:\Rightarrow \\ $$$${u}_{\mathrm{1}} =\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{e}^{{iarctan}\left(\frac{\mathrm{1}}{{t}}\right)} \:\:{and}\:{u}_{\mathrm{2}} =\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{e}^{−{iarctan}\left(\frac{\mathrm{1}}{{t}}\right)} \\ $$$${z}^{\mathrm{2}} ={u}_{\mathrm{1}} \Rightarrow{z}\:=\overset{−} {+}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)} \\ $$$$\mathrm{z}^{\mathrm{2}} =\mathrm{u}_{\mathrm{2}} \:\Rightarrow{z}\:=\overset{−} {+}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{t}\:}\right)} \:\Rightarrow \\ $$$${W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)\left({z}−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} {e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{t}}\right)} \left({z}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} {e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{t}}\right)} \right)\left({z}−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{t}}\right)} \right)\left({z}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right){e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{t}}\right)} \right)\right.} \\ $$$${residustheorem}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},\mathrm{2}{i}\right)\:+{Res}\left({W},\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)} \right.\right. \\ $$$$+\mathrm{R}{es}\left({W},−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{−\frac{{i}}{\mathrm{2}}{afctan}\left(\frac{\mathrm{1}}{{t}}\right)} \right\}…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *