Question Number 77886 by mathmax by abdo last updated on 11/Jan/20
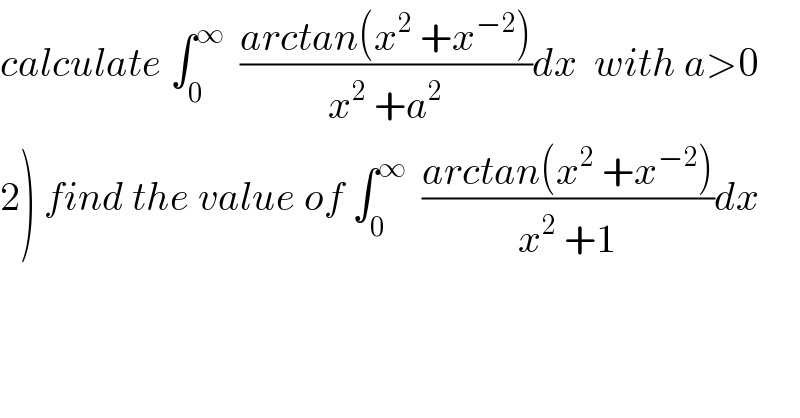
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} \:+{x}^{−\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} \:+{x}^{−\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$
Commented by mathmax by abdo last updated on 12/Jan/20

$$\left.\mathrm{1}\right)\:{let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:\:{the}\:{convergence}\:{of}\:{A}\:{is}\:{asdured} \\ $$$${because}\:\mid{arctan}\left({x}^{\mathrm{2}} \:+{x}^{−\mathrm{2}} \right)\mid<\frac{\pi}{\mathrm{2}}\:\:{for}\:{x}\neq\mathrm{0} \\ $$$${we}\:{have}\:\:\mathrm{2}{A}\:=\:\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} +{x}^{−\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:{let}\:{W}\left({z}\right)\:=\frac{{arctan}\left({z}^{\mathrm{2}} \:+{z}^{−\mathrm{2}} \right)}{{z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left({W},{ia}\right)\:=\mathrm{2}{i}\pi\frac{\mid{arctan}\left(−{a}^{\mathrm{2}} −\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)\mid}{\mathrm{2}{ia}} \\ $$$$=\frac{\pi}{{a}}{arctan}\left({a}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)\Rightarrow{A}\:=\frac{\pi}{\mathrm{2}{a}}{arctan}\left({a}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right) \\ $$$$\left.\mathrm{2}\right)\:{a}=\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} \:+{x}^{−\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:=\frac{\pi}{\mathrm{2}}{arctan}\left(\mathrm{2}\right). \\ $$
