Question Number 137693 by Mathspace last updated on 05/Apr/21
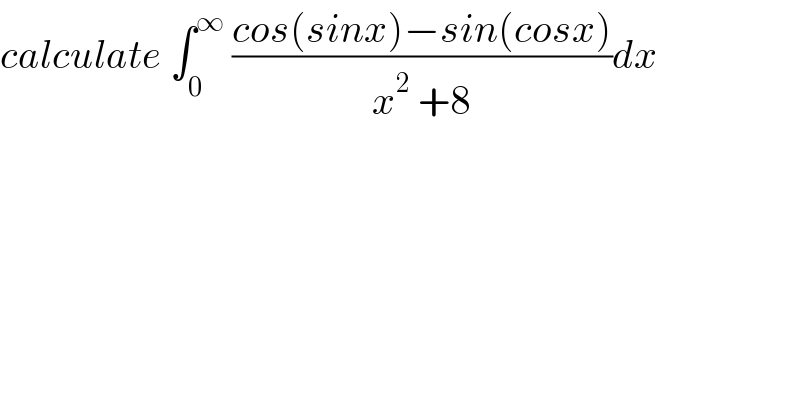
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({sinx}\right)−{sin}\left({cosx}\right)}{{x}^{\mathrm{2}} \:+\mathrm{8}}{dx} \\ $$
Answered by mathmax by abdo last updated on 07/Apr/21

$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sinx}\right)−\mathrm{sin}\left(\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{8}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{8}}\:\mathrm{dx}−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{8}}\mathrm{dx} \\ $$$$=\mathrm{I}−\mathrm{J} \\ $$$$\mathrm{I}\:=_{\mathrm{x}=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\right)\right.}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\mathrm{t}\:\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\right)\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\right)\right.}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{isin}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right)\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{isin}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{z}\right)} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{e}^{\mathrm{isin}\left(\mathrm{2i}\sqrt{\mathrm{2}}\right)} }{\mathrm{2i}}\:=\pi\:\mathrm{e}^{\mathrm{isin}\left(\mathrm{i2}\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{sinz}\:=\frac{\mathrm{e}^{\mathrm{iz}} −\mathrm{e}^{−\mathrm{iz}} }{\mathrm{2i}}\:\Rightarrow\mathrm{sin}\left(\mathrm{i2}\sqrt{\mathrm{2}}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{2i}\sqrt{\mathrm{2}}\right)} −\mathrm{e}^{−\mathrm{i}\left(\mathrm{2i}\sqrt{\mathrm{2}}\right)} }{\mathrm{2i}} \\ $$$$=\frac{\mathrm{e}^{−\mathrm{2}\sqrt{\mathrm{2}}} −\mathrm{e}^{\mathrm{2}\sqrt{\mathrm{2}}} }{\mathrm{2i}}\:=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{e}^{−\mathrm{2}\sqrt{\mathrm{2}}} \:−\mathrm{e}^{\left.\mathrm{2}\sqrt{\mathrm{2}}\right)} \:=\mathrm{ish}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\:\Rightarrow\right. \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\pi\:\mathrm{e}^{\mathrm{i}\left(\mathrm{ish}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\right.} \:=\pi\:\mathrm{e}^{−\mathrm{sh}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)} \:\:\Rightarrow\mathrm{I}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:\mathrm{e}^{−\mathrm{sh}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{changement}\:\mathrm{give}\:\mathrm{J}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\right)\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{icos}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\right)} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right)\:\mathrm{let}\:\Phi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{icos}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{z}\right)} }{\mathrm{z}^{\mathrm{2}\:} \:+\mathrm{1}}\mathrm{dt} \\ $$$$\int_{\mathrm{R}} \Phi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\Phi,\mathrm{i}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{e}^{\mathrm{icos}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i}\right)} }{\mathrm{2i}}\:=\pi\mathrm{e}^{\mathrm{ich}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$=\pi\left\{\mathrm{cos}\left(\mathrm{ch}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)+\mathrm{isin}\left(\mathrm{ch}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\right\}\:\Rightarrow\right.\right. \\ $$$$\mathrm{J}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{sin}\left(\mathrm{ch}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sinx}\right)−\mathrm{sin}\left(\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{8}}\mathrm{dx}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{e}^{−\mathrm{sh}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)} −\mathrm{sin}\left(\mathrm{ch}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\right)\right. \\ $$
