Menu Close

calculate-0-dx-x-2-3-x-2-8-2-

Tinku Tara 0 Comments
Pin




Question Number 66464 by mathmax by abdo last updated on 15/Aug/19
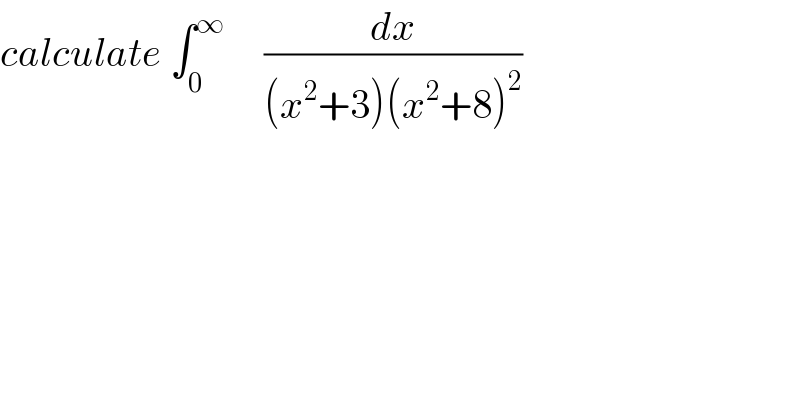
calculate ∫_0 ^∞ (dx/((x^2 +3)(x^2 +8)^2 ))
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{8}\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 16/Aug/19
let I =∫_0 ^∞ (dx/((x^2 +3)(x^2 +8)^2 )) ⇒2I =∫_(−∞) ^(+∞) (dx/((x^2 +3)(x^2 +8)^2 )) let ϕ(z)=(1/((z^2 +3)(z^2 +8)^2 )) poles of ϕ? ϕ(z) =(1/((z−i(√3))(z+i(√3))(z−i2(√2))^2 (z+i2(√2))^2 )) the poles of ϕ are +^− i(√3)and +^− 2i(√2) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{Res(ϕ,i(√3))+Res(ϕ,2i(√2))} Res(ϕ,i(√3)) =lim_(z→i(√3)) (z−i(√3))ϕ(z) =(1/(2i(√3)(−3+8)^2 )) =(1/(50i(√3))) Res(ϕ,2i(√2)) =lim_(z→2i(√2)) (1/((2−1)!)){(z−2i(√2))^2 ϕ(z)}^((1)) =lim_(z→2i(√2)) {(1/((z^2 +3)(z+2i(√2))^2 ))}^((1)) =lim_(z→2i(√2)) −((2z(z+2i(√2))^2 +2(z+2i(√2))(z^2 +3))/((z^2 +3)^2 (z+2i(√2))^2 )) =lim_(z→2i(√2)) −((2z(z+2i(√2))+2(z^2 +3))/((z^2 +3)^2 (z+2i(√2)))) =−((4i(√2)(4i(√2))+2(−8+3))/((−8+3)^2 (4i(√2)))) =−((−32−10)/(100i(√2))) =((42)/(100i(√2))) =((21)/(50i(√2))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{(1/(50i(√3)))+((21)/(50i(√2)))} =(π/(25(√3))) +((21π)/(25(√2))) =2I
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{2}} \:+\mathrm{8}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{8}\right)^{\mathrm{2}} } \\ $$$${let}\:\varphi\left({z}\right)=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)\left({z}^{\mathrm{2}} \:+\mathrm{8}\right)^{\mathrm{2}} }\:\:{poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\sqrt{\mathrm{3}}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)\left({z}−{i}\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left({z}+{i}\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:\:{the}\:{poles}\:{of}\:\varphi\:{are} \\ $$$$\overset{−} {+}{i}\sqrt{\mathrm{3}}{and}\:\overset{−} {+}\mathrm{2}{i}\sqrt{\mathrm{2}}\:\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{{Res}\left(\varphi,{i}\sqrt{\mathrm{3}}\right)+{Res}\left(\varphi,\mathrm{2}{i}\sqrt{\mathrm{2}}\right)\right\} \\ $$$${Res}\left(\varphi,{i}\sqrt{\mathrm{3}}\right)\:={lim}_{{z}\rightarrow{i}\sqrt{\mathrm{3}}} \:\:\:\left({z}−{i}\sqrt{\mathrm{3}}\right)\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left(−\mathrm{3}+\mathrm{8}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{50}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,\mathrm{2}{i}\sqrt{\mathrm{2}}\right)\:={lim}_{{z}\rightarrow\mathrm{2}{i}\sqrt{\mathrm{2}}} \:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\mathrm{2}{i}\sqrt{\mathrm{2}}} \:\:\:\:\:\left\{\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)\left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\mathrm{2}{i}\sqrt{\mathrm{2}}} \:\:\:−\frac{\mathrm{2}{z}\left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{2}\left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)}{\left({z}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} \left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$={lim}_{{z}\rightarrow\mathrm{2}{i}\sqrt{\mathrm{2}}} \:\:\:\:−\frac{\mathrm{2}{z}\left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)+\mathrm{2}\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)}{\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} \left({z}+\mathrm{2}{i}\sqrt{\mathrm{2}}\right)} \\ $$$$=−\frac{\mathrm{4}{i}\sqrt{\mathrm{2}}\left(\mathrm{4}{i}\sqrt{\mathrm{2}}\right)+\mathrm{2}\left(−\mathrm{8}+\mathrm{3}\right)}{\left(−\mathrm{8}+\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{4}{i}\sqrt{\mathrm{2}}\right)}\:=−\frac{−\mathrm{32}−\mathrm{10}}{\mathrm{100}{i}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{42}}{\mathrm{100}{i}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{21}}{\mathrm{50}{i}\sqrt{\mathrm{2}}} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{\mathrm{1}}{\mathrm{50}{i}\sqrt{\mathrm{3}}}+\frac{\mathrm{21}}{\mathrm{50}{i}\sqrt{\mathrm{2}}}\right\}\:=\frac{\pi}{\mathrm{25}\sqrt{\mathrm{3}}}\:+\frac{\mathrm{21}\pi}{\mathrm{25}\sqrt{\mathrm{2}}}\:=\mathrm{2}{I} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *