Menu Close

calculate-0-e-3x-2-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 142989 by mathmax by abdo last updated on 08/Jun/21
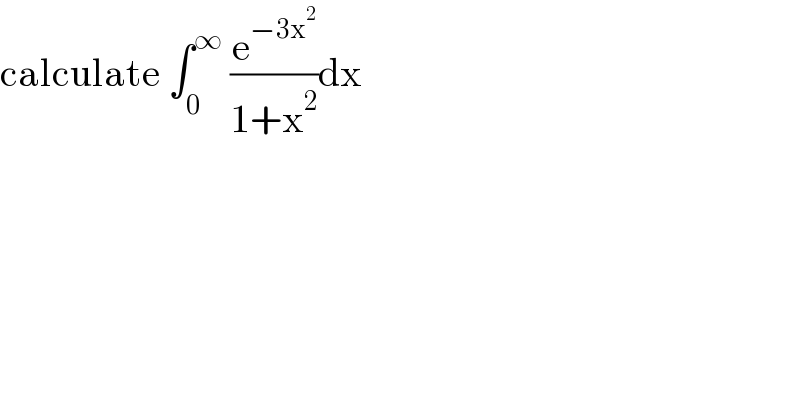
calculate ∫_0 ^∞ (e^(−3x^2 ) /(1+x^2 ))dx
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{3x}^{\mathrm{2}} } }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Jun/21
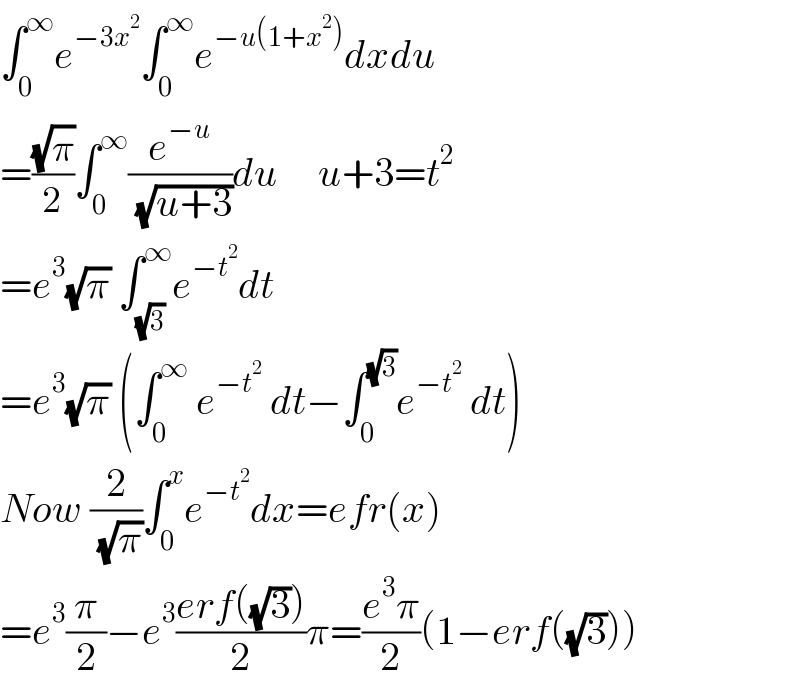
∫_0 ^∞ e^(−3x^2 ) ∫_0 ^∞ e^(−u(1+x^2 )) dxdu =((√π)/2)∫_0 ^∞ (e^(−u) /( (√(u+3))))du u+3=t^2 =e^3 (√π) ∫_(√3) ^∞ e^(−t^2 ) dt =e^3 (√π) (∫_0 ^∞ e^(−t^2 ) dt−∫_0 ^(√3) e^(−t^2 ) dt) Now (2/( (√π)))∫_0 ^x e^(−t^2 ) dx=efr(x) =e^3 (π/2)−e^3 ((erf((√3)))/2)π=((e^3 π)/2)(1−erf((√3)))
$$\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{x}^{\mathrm{2}} } \int_{\mathrm{0}} ^{\infty} {e}^{−{u}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} {dxdu} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{u}} }{\:\sqrt{{u}+\mathrm{3}}}{du}\:\:\:\:\:{u}+\mathrm{3}={t}^{\mathrm{2}} \\ $$$$={e}^{\mathrm{3}} \sqrt{\pi}\:\int_{\sqrt{\mathrm{3}}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$={e}^{\mathrm{3}} \sqrt{\pi}\:\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}^{\mathrm{2}} } \:{dt}−\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} {e}^{−{t}^{\mathrm{2}} } \:{dt}\right) \\ $$$${Now}\:\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{{x}} {e}^{−{t}^{\mathrm{2}} } {dx}={efr}\left({x}\right) \\ $$$$={e}^{\mathrm{3}} \frac{\pi}{\mathrm{2}}−{e}^{\mathrm{3}} \frac{{erf}\left(\sqrt{\mathrm{3}}\right)}{\mathrm{2}}\pi=\frac{{e}^{\mathrm{3}} \pi}{\mathrm{2}}\left(\mathrm{1}−{erf}\left(\sqrt{\mathrm{3}}\right)\right) \\ $$
Answered by mathmax by abdo last updated on 09/Jun/21
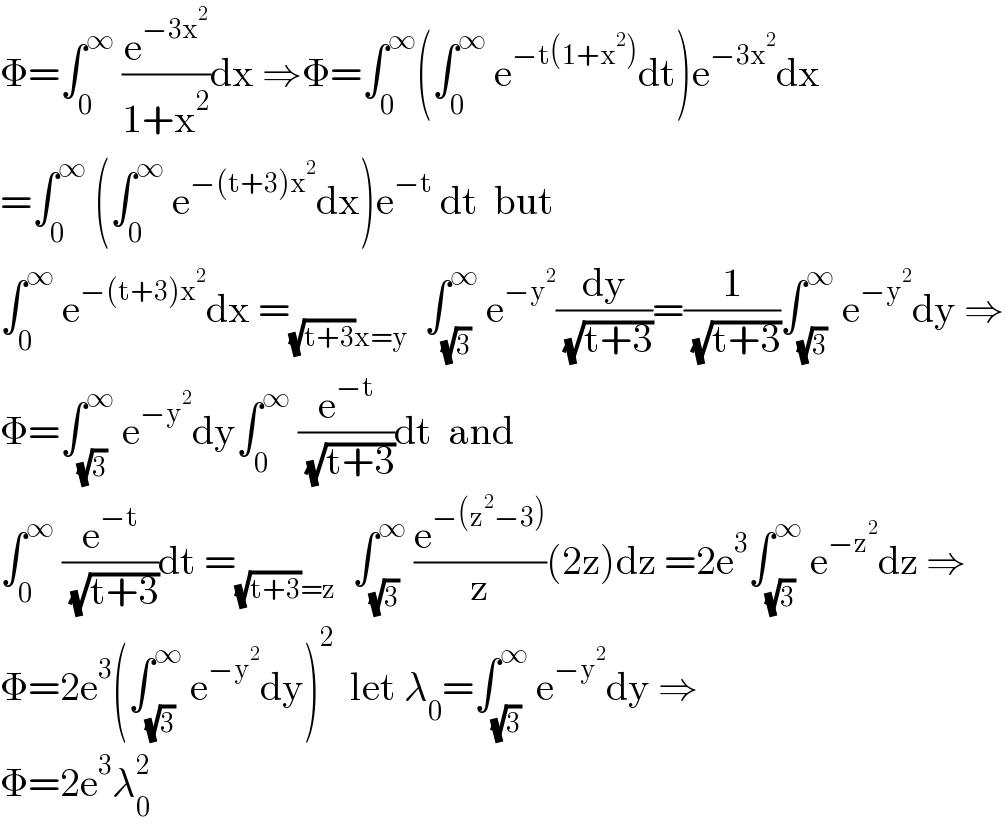
Φ=∫_0 ^∞ (e^(−3x^2 ) /(1+x^2 ))dx ⇒Φ=∫_0 ^∞ (∫_0 ^∞ e^(−t(1+x^2 )) dt)e^(−3x^2 ) dx =∫_0 ^∞ (∫_0 ^∞ e^(−(t+3)x^2 ) dx)e^(−t) dt but ∫_0 ^∞ e^(−(t+3)x^2 ) dx =_((√(t+3))x=y) ∫_(√3) ^∞ e^(−y^2 ) (dy/( (√(t+3))))=(1/( (√(t+3))))∫_(√3) ^∞ e^(−y^2 ) dy ⇒ Φ=∫_(√3) ^∞ e^(−y^2 ) dy∫_0 ^∞ (e^(−t) /( (√(t+3))))dt and ∫_0 ^∞ (e^(−t) /( (√(t+3))))dt =_((√(t+3))=z) ∫_(√3) ^∞ (e^(−(z^2 −3)) /z)(2z)dz =2e^3 ∫_(√3) ^∞ e^(−z^2 ) dz ⇒ Φ=2e^3 (∫_(√3) ^∞ e^(−y^2 ) dy)^2 let λ_0 =∫_(√3) ^∞ e^(−y^2 ) dy ⇒ Φ=2e^3 λ_0 ^2
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{3x}^{\mathrm{2}} } }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \mathrm{dt}\right)\mathrm{e}^{−\mathrm{3x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{t}+\mathrm{3}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\right)\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{t}+\mathrm{3}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=_{\sqrt{\mathrm{t}+\mathrm{3}}\mathrm{x}=\mathrm{y}} \:\:\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \frac{\mathrm{dy}}{\:\sqrt{\mathrm{t}+\mathrm{3}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}+\mathrm{3}}}\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\:\Rightarrow \\ $$$$\Phi=\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}+\mathrm{3}}}\mathrm{dt}\:\:\mathrm{and}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}+\mathrm{3}}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}+\mathrm{3}}=\mathrm{z}} \:\:\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\frac{\mathrm{e}^{−\left(\mathrm{z}^{\mathrm{2}} −\mathrm{3}\right)} }{\mathrm{z}}\left(\mathrm{2z}\right)\mathrm{dz}\:=\mathrm{2e}^{\mathrm{3}} \int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:\Rightarrow \\ $$$$\Phi=\mathrm{2e}^{\mathrm{3}} \left(\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\right)^{\mathrm{2}} \:\:\mathrm{let}\:\lambda_{\mathrm{0}} =\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\:\Rightarrow \\ $$$$\Phi=\mathrm{2e}^{\mathrm{3}} \lambda_{\mathrm{0}} ^{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *