Question Number 72011 by mathmax by abdo last updated on 23/Oct/19
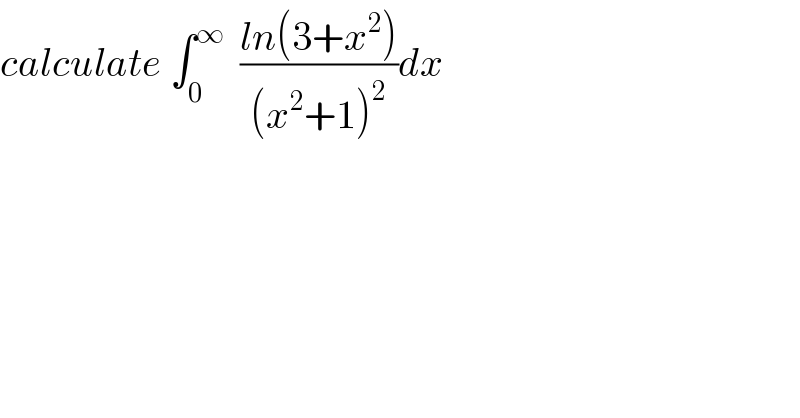
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 25/Oct/19

$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:{let} \\ $$$${f}\left({z}\right)=\frac{{ln}\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{f}\left({z}\right)\:=\frac{{ln}\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}{\left({z}−{i}\right)^{\mathrm{2}} \left({z}+{i}\right)^{\mathrm{2}} }\:{so}\:{the}\:{poles}\:{of}\:{f}\:{are}\:{i} \\ $$$${and}\:−{i}\:\:\left({doubles}\right)\:{residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left({f},{i}\right) \\ $$$${Res}\left({f},{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{i}\right)^{\mathrm{2}} {f}\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\left\{\frac{{ln}\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}{\left({z}+{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} ={lim}_{{z}\rightarrow{i}} \:\:\:\frac{\frac{\mathrm{2}{z}}{\mathrm{3}+{z}^{\mathrm{2}} }×\left({z}+{i}\right)^{\mathrm{2}} −\mathrm{2}\left({z}+{i}\right){ln}\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}{\left({z}+{i}\right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\:\:\frac{\frac{\mathrm{2}{z}\left({z}+{i}\right)}{\mathrm{3}+{z}^{\mathrm{2}} }−\mathrm{2}{ln}\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}{\left({z}+{i}\right)^{\mathrm{3}} }\:=\frac{\frac{\mathrm{2}{i}\left(\mathrm{2}{i}\right)}{\mathrm{2}}−\mathrm{2}{ln}\left(\mathrm{2}\right)}{\left(\mathrm{2}{i}\right)^{\mathrm{3}} }=\frac{−\mathrm{2}−\mathrm{2}{ln}\left(\mathrm{2}\right)}{−\mathrm{8}{i}} \\ $$$$=\frac{\mathrm{1}+{ln}\left(\mathrm{2}\right)}{\mathrm{4}{i}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi×\frac{\mathrm{1}+{ln}\left(\mathrm{2}\right)}{\mathrm{4}{i}}\:=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{ln}\left(\mathrm{2}\right)\right) \\ $$$$=\mathrm{2}{A}\:\Rightarrow\:{A}\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+{ln}\left(\mathrm{2}\right)\right) \\ $$
Answered by mind is power last updated on 23/Oct/19
![let f(t)=∫_0 ^(+∞) ((ln(t+x^2 ))/((x^2 +1)^2 ))dx,t≥3 f′(t)=∫_0 ^(+∞) (dx/((t+x^2 )(1+x^2 )^2 )) f′(t)=(1/2)∫_(−∞) ^(+∞) (dx/((t+x^2 )(1+x^2 )^2 )) letΓ= C_R ∪[−R,R] our contor C_R =Re^(iθ) ,0≤θ≤π ∫_Γ (dx/((t+x^2 )(1+x^2 )^2 ))=2iπ(Res(f,i(√t))+res(f,i)) Res(f,i(√t))=(1/((1−t)^2 .2i(√t))) Res(f,i)=(d/dx)(((x−i)^2 )/((t+x^2 )(x+i)^2 (x−i)^2 ))∣_(x=i) =(d/dx)((1/((t+x^2 )(x+i)^2 )))=((−2x(x+i)^2 −2(x+i)(t+x^2 ))/((t+x^2 )^2 (x+i)^4 ))∣x=i =((−2i(2i)^2 −4i(t−1))/((t−1)^2 (16)))=((12i−4it)/(16(t−1)^2 )).=((−i(t−3))/(4(t−1)^2 )) f′(t)=(1/2)∫_(−∞) ^(+∞) (dx/((t+x^2 )(1+x^2 )^2 ))=iπ.((1/((1−t)^2 2i(√t)))−((i(t−3))/(4(t−1)^2 ))) =(π/((1−t)^2 .2(√t)))+((π(t−1−2))/(4(t−1)^2 ))dt f(t)=∫((πdt)/((1−t)^2 .2(√t)))+∫(π/(4(t−1)))dt−(π/2)∫(dt/((t−1)^2 )) for first u=(√t)⇒du=(1/(2(√t)))dt f(t)=(π/4)ln(∣t−1∣)+(π/(2(t−1)))+∫((πdu)/((1−u)^2 (1+u)^2 )) (a/(1−u))+(b/(1+u))+(π/(4(1+u)^2 ))+(π/(4(1−u)^2 )) b−a=π b+a=(π/2) b=((3π)/4),a=−(π/4) f(t)=(π/4)ln(∣t−1∣)+(π/(2(t−1)))+∫((−π)/(4(1−u)))dt+∫((3π)/(4(1+u)))+(π/4)∫(1/((1+u)^2 ))+(1/((1−u)^2 ))du after integration and put u=(√t) f(t)=(π/4)ln(∣t−1∣)+(π/(2(t−1)))+(π/4)ln(∣(√t)−1∣)+((3π)/4)ln(1+(√t))−(π/(4(1+(√t))))+(π/(4(1−(√(t)))))+c f(0)=∫_0 ^(+∞) ((ln(x^2 ))/((1+x^2 )^2 )) residus theorem ∫_(−R) ^(−ε) ((ln(z^2 ))/((1+z^2 )^2 ))dz+∫_C_ε ((ln(z^2 ))/((1+z^2 )^2 ))dz+∫_ε ^R ((ln(z^2 ))/((1+z^2 )^2 ))dz+∫_0 ^π .((ln(R^2 e^(i2θ)) ))/((1+R^2 e^(2iθ) )^2 )).Rie^(iθ) dθ ∫_(−R) ^(−ε) ((ln(z^2 ))/((1+z^2 )^2 ))dz=∫_ε ^R ((2ln(z)+iπ)/((1+z^2 )^2 ))dz ∫_(Cε) ((ln(z^2 ))/((1+z^2 )^2 ))dz=∫_π ^0 ((ln(ε^2 e^(2iθ) ))/((1+ε^2 e^(2iθ) )^2 )).εie^(iθ) dθ ∣ln(re^(iθ) )∣=∣ln(r)+iθ∣=(√((ln(r))^2 +θ^2 )) ∣1+εe^(iθ) ∣≥∣1−ε∣⇒ ∣∫_(Cε) ((ln(z^2 ))/((1+z^2 )^2 ))dz∣=∫_0 ^π ∣((ln(ε^2 e^(2iθ) ))/((1+ε^2 e^(2iθ) )^2 )).εie^(iθ) dθ∣≤((ε(√((ln(r))^2 +θ^2 )))/((1−ε^2 )^2 )).π→_(ε→0) 0 meme idee marche pour R→∞ ⇒∫_Γ ((ln(z^2 ))/((1+z^2 )^2 ))dz=2∫_0 ^(+∞) ((ln(z^2 ))/((1+z^2 )^2 ))+∫((2iπ)/((1+z^2 )^2 ))dz=2iπ Res(f,i) Res(f,i)=(d/dz).((ln(z^2 ))/((z+i)^2 ))∣_(z=i) =(((2/z).(z+i)^2 −2(z+i)ln(z^2 ))/((z+i)^4 ))=((−2i(2i)^2 −4iln(−1))/((2i)^4 ))=((8i+4π)/(16)) ⇒2∫_0 ^(+∞) ((ln(z^2 ))/((1+z^2 )^2 ))dz=2iπ.(((8i)/(16)))=−π ⇒∫_0 ^∞ ((ln(z^2 ))/((1+z^2 )))dz=((−π)/2) ⇒f(0)=−(π/2) f(t)=(π/4)ln(∣t−1∣)+(π/(2(t−1)))+(π/4)ln(∣(√t)−1∣)+((3π)/4)ln(1+(√t))−(π/(4(1+(√t))))+(π/(4(1−(√(t)))))+c ⇒f(0)=−(π/2)+(π/4)+(π/4)+c=−(π/2)⇒c=−(π/2) ∫_0 ^(+∞) ((ln(3+x^2 ))/((1+x^2 )^2 ))dx=f(3)](https://www.tinkutara.com/question/Q72065.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx},\mathrm{t}\geqslant\mathrm{3} \\ $$$$\mathrm{f}'\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{f}'\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{let}\Gamma=\:\mathrm{C}_{\mathrm{R}} \cup\left[−\mathrm{R},\mathrm{R}\right]\:\mathrm{our}\:\mathrm{contor}\:\mathrm{C}_{\mathrm{R}} =\mathrm{Re}^{\mathrm{i}\theta} ,\mathrm{0}\leqslant\theta\leqslant\pi \\ $$$$\int_{\Gamma} \frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{2i}\pi\left(\mathrm{Res}\left(\mathrm{f},\mathrm{i}\sqrt{\mathrm{t}}\right)+\mathrm{res}\left(\mathrm{f},\mathrm{i}\right)\right) \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\sqrt{\mathrm{t}}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} .\mathrm{2i}\sqrt{\mathrm{t}}} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\frac{\mathrm{d}}{\mathrm{dx}}\frac{\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} }{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} }\mid_{\mathrm{x}=\mathrm{i}} \\ $$$$=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} }\right)=\frac{−\mathrm{2x}\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{x}+\mathrm{i}\right)\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{4}} }\mid\mathrm{x}=\mathrm{i} \\ $$$$=\frac{−\mathrm{2i}\left(\mathrm{2i}\right)^{\mathrm{2}} −\mathrm{4i}\left(\mathrm{t}−\mathrm{1}\right)}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{16}\right)}=\frac{\mathrm{12i}−\mathrm{4it}}{\mathrm{16}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }.=\frac{−\mathrm{i}\left(\mathrm{t}−\mathrm{3}\right)}{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{f}'\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{i}\pi.\left(\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \mathrm{2i}\sqrt{\mathrm{t}}}−\frac{\mathrm{i}\left(\mathrm{t}−\mathrm{3}\right)}{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} .\mathrm{2}\sqrt{\mathrm{t}}}+\frac{\pi\left(\mathrm{t}−\mathrm{1}−\mathrm{2}\right)}{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\int\frac{\pi\mathrm{dt}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} .\mathrm{2}\sqrt{\mathrm{t}}}+\int\frac{\pi}{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)}\mathrm{dt}−\frac{\pi}{\mathrm{2}}\int\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{for}\:\mathrm{first}\:\mathrm{u}=\sqrt{\mathrm{t}}\Rightarrow\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{t}}}\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\mathrm{t}−\mathrm{1}\mid\right)+\frac{\pi}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\int\frac{\pi\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{a}}{\mathrm{1}−\mathrm{u}}+\frac{\mathrm{b}}{\mathrm{1}+\mathrm{u}}+\frac{\pi}{\mathrm{4}\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }+\frac{\pi}{\mathrm{4}\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{b}−\mathrm{a}=\pi \\ $$$$\mathrm{b}+\mathrm{a}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{b}=\frac{\mathrm{3}\pi}{\mathrm{4}},\mathrm{a}=−\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\mathrm{t}−\mathrm{1}\mid\right)+\frac{\pi}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\int\frac{−\pi}{\mathrm{4}\left(\mathrm{1}−\mathrm{u}\right)}\mathrm{dt}+\int\frac{\mathrm{3}\pi}{\mathrm{4}\left(\mathrm{1}+\mathrm{u}\right)}+\frac{\pi}{\mathrm{4}}\int\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$\mathrm{after}\:\mathrm{integration}\:\mathrm{and}\:\mathrm{put}\:\mathrm{u}=\sqrt{\mathrm{t}} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\mathrm{t}−\mathrm{1}\mid\right)+\frac{\pi}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\sqrt{\mathrm{t}}−\mathrm{1}\mid\right)+\frac{\mathrm{3}\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{t}}\right)−\frac{\pi}{\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{t}}\right)}+\frac{\pi}{\mathrm{4}\left(\mathrm{1}−\sqrt{\left.\mathrm{t}\right)}\right.}+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{residus}\:\mathrm{theorem} \\ $$$$\int_{−\mathrm{R}} ^{−\epsilon} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}+\int_{\mathrm{C}_{\epsilon} } \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}+\int_{\epsilon} ^{\mathrm{R}} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}+\int_{\mathrm{0}} ^{\pi} .\frac{\mathrm{ln}\left(\mathrm{R}^{\mathrm{2}} \mathrm{e}^{\left.\mathrm{i2}\theta\right)} \right)}{\left(\mathrm{1}+\mathrm{R}^{\mathrm{2}} \mathrm{e}^{\mathrm{2i}\theta} \right)^{\mathrm{2}} }.\mathrm{Rie}^{\mathrm{i}\theta} \mathrm{d}\theta \\ $$$$\int_{−\mathrm{R}} ^{−\epsilon} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}=\int_{\epsilon} ^{\mathrm{R}} \frac{\mathrm{2ln}\left(\mathrm{z}\right)+\mathrm{i}\pi}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz} \\ $$$$\int_{\mathrm{C}\epsilon} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}=\int_{\pi} ^{\mathrm{0}} \frac{\mathrm{ln}\left(\epsilon^{\mathrm{2}} \mathrm{e}^{\mathrm{2i}\theta} \right)}{\left(\mathrm{1}+\epsilon^{\mathrm{2}} \mathrm{e}^{\mathrm{2i}\theta} \right)^{\mathrm{2}} }.\epsilon\mathrm{ie}^{\mathrm{i}\theta} \mathrm{d}\theta \\ $$$$\mid\mathrm{ln}\left(\mathrm{re}^{\mathrm{i}\theta} \right)\mid=\mid\mathrm{ln}\left(\mathrm{r}\right)+\mathrm{i}\theta\mid=\sqrt{\left(\mathrm{ln}\left(\mathrm{r}\right)\right)^{\mathrm{2}} +\theta^{\mathrm{2}} } \\ $$$$\mid\mathrm{1}+\epsilon\mathrm{e}^{\mathrm{i}\theta} \mid\geqslant\mid\mathrm{1}−\epsilon\mid\Rightarrow \\ $$$$\mid\int_{\mathrm{C}\epsilon} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}\mid=\int_{\mathrm{0}} ^{\pi} \mid\frac{\mathrm{ln}\left(\epsilon^{\mathrm{2}} \mathrm{e}^{\mathrm{2i}\theta} \right)}{\left(\mathrm{1}+\epsilon^{\mathrm{2}} \mathrm{e}^{\mathrm{2i}\theta} \right)^{\mathrm{2}} }.\epsilon\mathrm{ie}^{\mathrm{i}\theta} \mathrm{d}\theta\mid\leqslant\frac{\epsilon\sqrt{\left(\mathrm{ln}\left(\mathrm{r}\right)\right)^{\mathrm{2}} +\theta^{\mathrm{2}} }}{\left(\mathrm{1}−\epsilon^{\mathrm{2}} \right)^{\mathrm{2}} }.\pi\underset{\epsilon\rightarrow\mathrm{0}} {\rightarrow}\mathrm{0} \\ $$$$\mathrm{meme}\:\mathrm{idee}\:\mathrm{marche}\:\mathrm{pour}\:\mathrm{R}\rightarrow\infty \\ $$$$\Rightarrow\int_{\Gamma} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }+\int\frac{\mathrm{2i}\pi}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right) \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\frac{\mathrm{d}}{\mathrm{dz}}.\frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\mid_{\mathrm{z}=\mathrm{i}} \\ $$$$=\frac{\frac{\mathrm{2}}{\mathrm{z}}.\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }=\frac{−\mathrm{2i}\left(\mathrm{2i}\right)^{\mathrm{2}} −\mathrm{4iln}\left(−\mathrm{1}\right)}{\left(\mathrm{2i}\right)^{\mathrm{4}} }=\frac{\mathrm{8i}+\mathrm{4}\pi}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dz}=\mathrm{2i}\pi.\left(\frac{\mathrm{8i}}{\mathrm{16}}\right)=−\pi \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\mathrm{dz}=\frac{−\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=−\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\mathrm{t}−\mathrm{1}\mid\right)+\frac{\pi}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mid\sqrt{\mathrm{t}}−\mathrm{1}\mid\right)+\frac{\mathrm{3}\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{t}}\right)−\frac{\pi}{\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{t}}\right)}+\frac{\pi}{\mathrm{4}\left(\mathrm{1}−\sqrt{\left.\mathrm{t}\right)}\right.}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=−\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}+\mathrm{c}=−\frac{\pi}{\mathrm{2}}\Rightarrow\mathrm{c}=−\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{3}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{f}\left(\mathrm{3}\right) \\ $$
Commented by mathmax by abdo last updated on 25/Oct/19

$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 25/Oct/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
