Menu Close

calculate-0-logx-1-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 141220 by mathmax by abdo last updated on 16/May/21
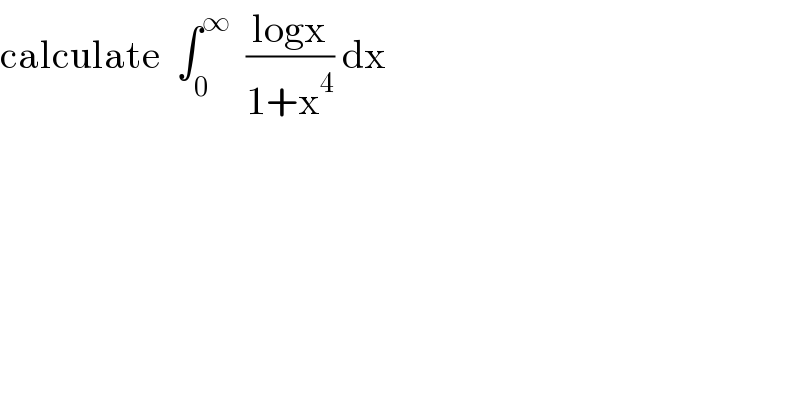
calculate ∫_0 ^∞ ((logx)/(1+x^4 )) dx
$$\mathrm{calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 16/May/21
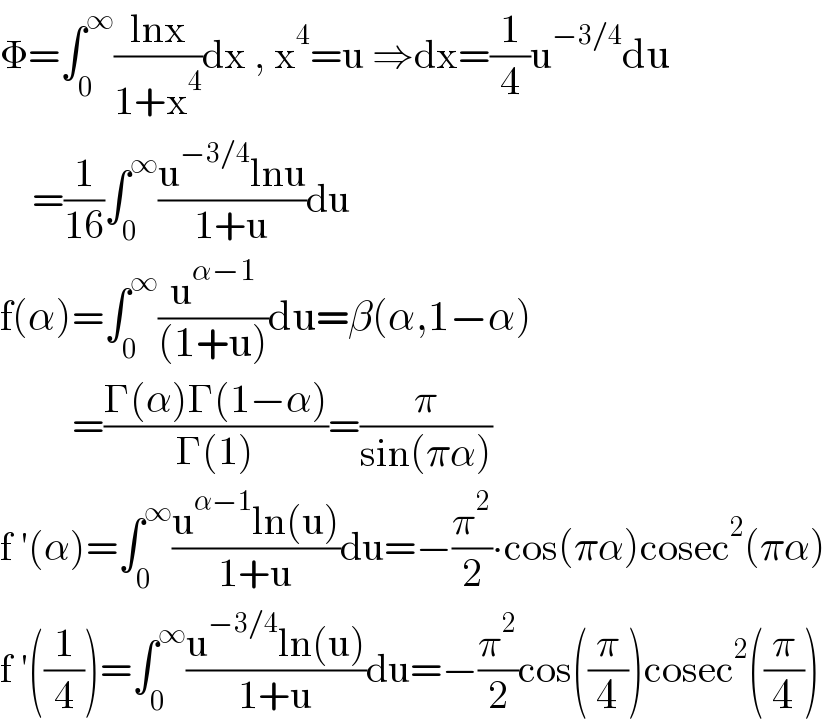
Φ=∫_0 ^∞ ((lnx)/(1+x^4 ))dx , x^4 =u ⇒dx=(1/4)u^(−3/4) du =(1/(16))∫_0 ^∞ ((u^(−3/4) lnu)/(1+u))du f(α)=∫_0 ^∞ (u^(α−1) /((1+u)))du=β(α,1−α) =((Γ(α)Γ(1−α))/(Γ(1)))=(π/(sin(πα))) f ′(α)=∫_0 ^∞ ((u^(α−1) ln(u))/(1+u))du=−(π^2 /2)∙cos(πα)cosec^2 (πα) f ′((1/4))=∫_0 ^∞ ((u^(−3/4) ln(u))/(1+u))du=−(π^2 /2)cos((π/4))cosec^2 ((π/4))
$$\Phi=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:,\:\mathrm{x}^{\mathrm{4}} =\mathrm{u}\:\Rightarrow\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{u}^{−\mathrm{3}/\mathrm{4}} \mathrm{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\mathrm{3}/\mathrm{4}} \mathrm{lnu}}{\mathrm{1}+\mathrm{u}}\mathrm{du} \\ $$$$\mathrm{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\alpha−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{u}\right)}\mathrm{du}=\beta\left(\alpha,\mathrm{1}−\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\Gamma\left(\alpha\right)\Gamma\left(\mathrm{1}−\alpha\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{\mathrm{sin}\left(\pi\alpha\right)} \\ $$$$\mathrm{f}\:'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\alpha−\mathrm{1}} \mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du}=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\centerdot\mathrm{cos}\left(\pi\alpha\right)\mathrm{cosec}^{\mathrm{2}} \left(\pi\alpha\right) \\ $$$$\mathrm{f}\:'\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\mathrm{3}/\mathrm{4}} \mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du}=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\right)\mathrm{cosec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right) \\ $$
Answered by mathmax by abdo last updated on 16/May/21
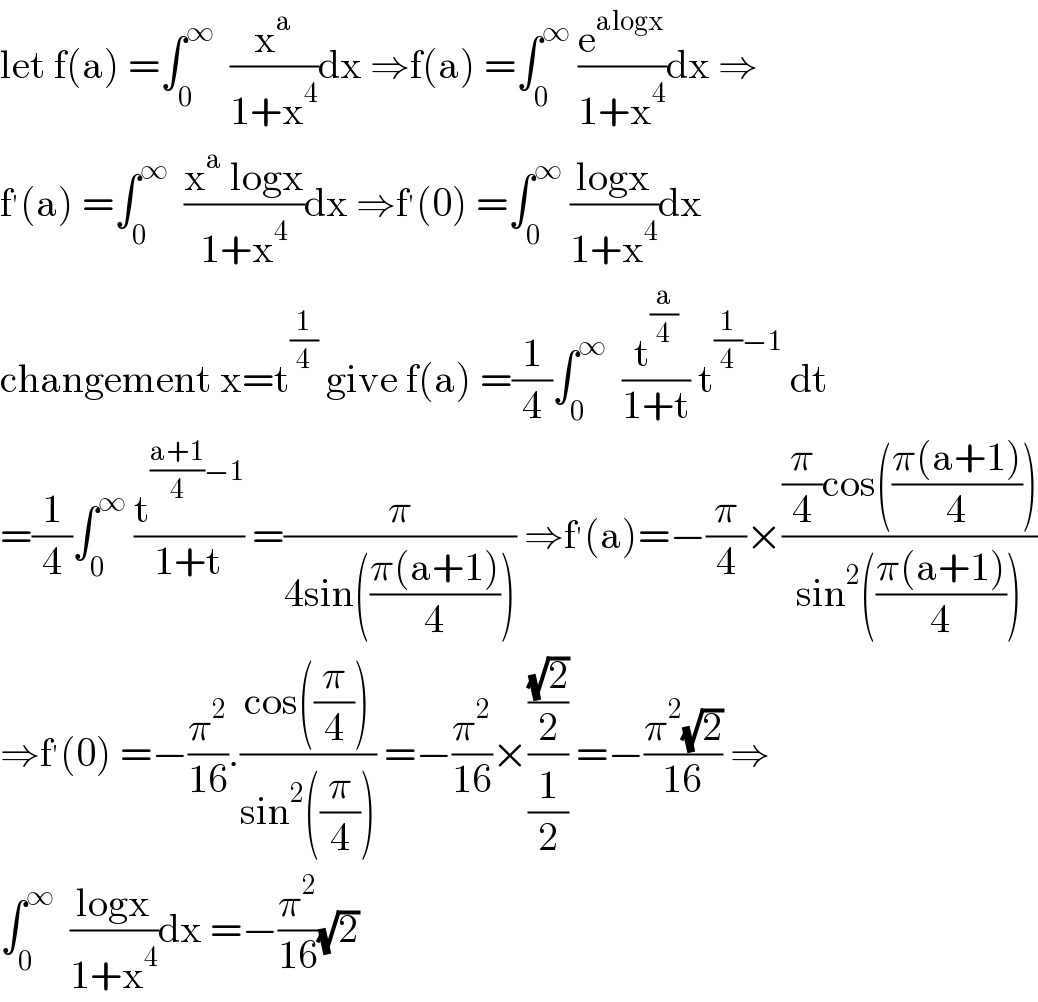
let f(a) =∫_0 ^∞ (x^a /(1+x^4 ))dx ⇒f(a) =∫_0 ^∞ (e^(alogx) /(1+x^4 ))dx ⇒ f^′ (a) =∫_0 ^∞ ((x^a logx)/(1+x^4 ))dx ⇒f^′ (0) =∫_0 ^∞ ((logx)/(1+x^4 ))dx changement x=t^(1/4) give f(a) =(1/4)∫_0 ^∞ (t^(a/4) /(1+t)) t^((1/4)−1) dt =(1/4)∫_0 ^∞ (t^(((a+1)/4)−1) /(1+t)) =(π/(4sin(((π(a+1))/4)))) ⇒f^′ (a)=−(π/4)×(((π/4)cos(((π(a+1))/4)))/(sin^2 (((π(a+1))/4)))) ⇒f^′ (0) =−(π^2 /(16)).((cos((π/4)))/(sin^2 ((π/4)))) =−(π^2 /(16))×(((√2)/2)/(1/2)) =−((π^2 (√2))/(16)) ⇒ ∫_0 ^∞ ((logx)/(1+x^4 ))dx =−(π^2 /(16))(√2)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{a}} }{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{alogx}} }{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{a}} \:\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$\mathrm{changement}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{give}\:\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{4}}} }{\mathrm{1}+\mathrm{t}}\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\:=\frac{\pi}{\mathrm{4sin}\left(\frac{\pi\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{4}}\right)}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\pi}{\mathrm{4}}×\frac{\frac{\pi}{\mathrm{4}}\mathrm{cos}\left(\frac{\pi\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{4}}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{4}}\right)} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}.\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right)}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}×\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}\:=−\frac{\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{16}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\sqrt{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *