Question Number 136036 by mathmax by abdo last updated on 18/Mar/21
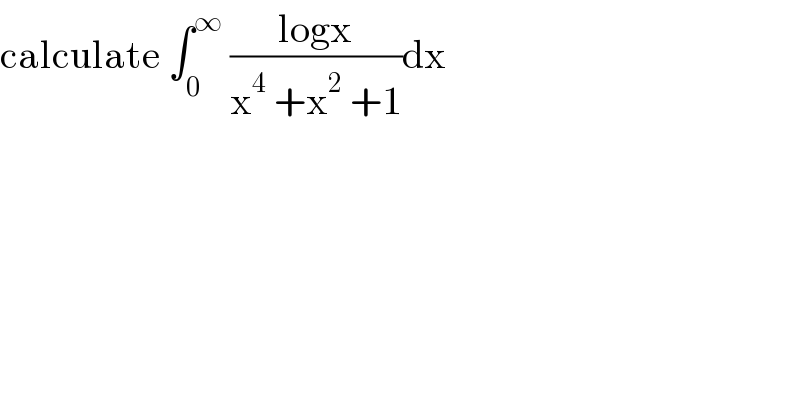
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$
Commented by Ajetunmobi last updated on 18/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{hi}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{chat}}\:\boldsymbol{\mathrm{privately}}\:? \\ $$
Commented by Ajetunmobi last updated on 18/Mar/21

Commented by liki last updated on 19/Mar/21
$$\mathrm{Drop}\:\mathrm{your}\:\mathrm{whatssap}\:\mathrm{number}\:\mathrm{here}\:! \\ $$
Commented by mathmax by abdo last updated on 31/May/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{liki}… \\ $$
Answered by Ar Brandon last updated on 18/Mar/21
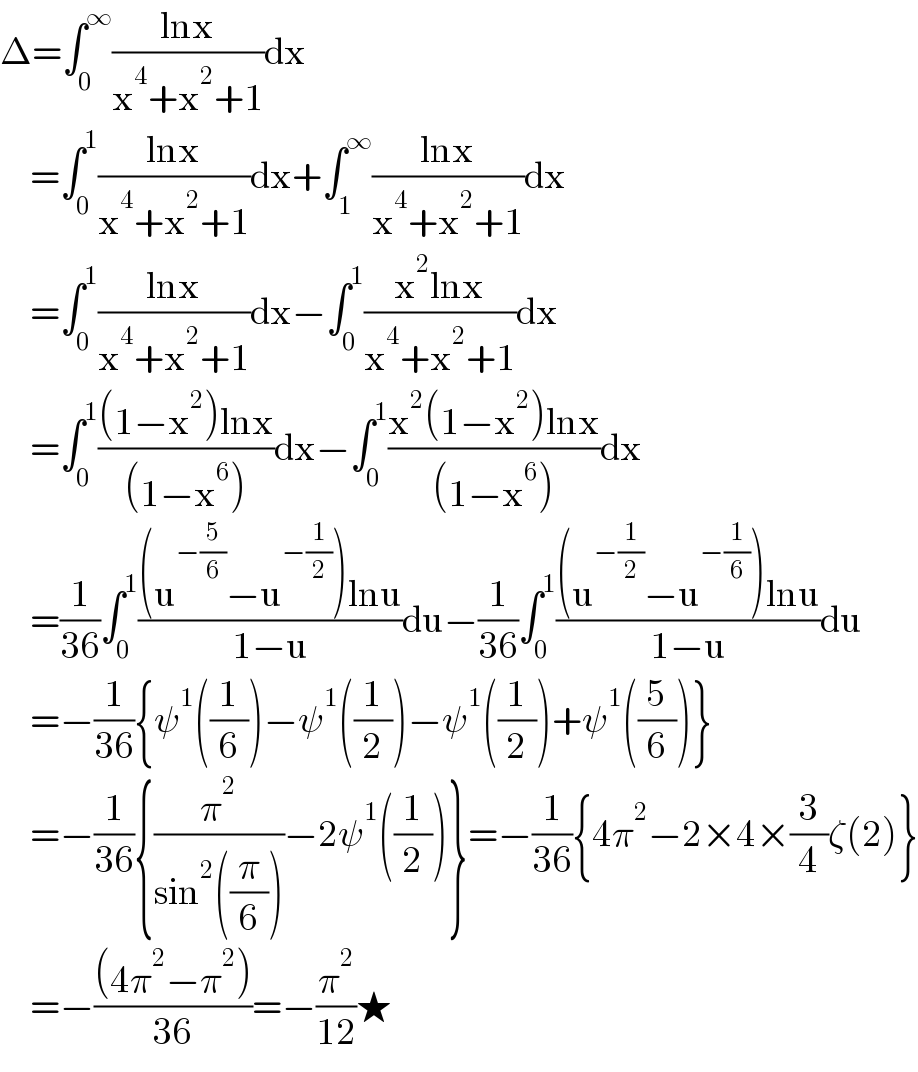
$$\Delta=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{6}} \right)}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{6}} \right)}\mathrm{dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} −\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)\mathrm{lnu}}{\mathrm{1}−\mathrm{u}}\mathrm{du}−\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{6}}} \right)\mathrm{lnu}}{\mathrm{1}−\mathrm{u}}\mathrm{du} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{36}}\left\{\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)−\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)\right\} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{36}}\left\{\frac{\pi^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{6}}\right)}−\mathrm{2}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right\}=−\frac{\mathrm{1}}{\mathrm{36}}\left\{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}×\mathrm{4}×\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)\right\} \\ $$$$\:\:\:\:\:=−\frac{\left(\mathrm{4}\pi^{\mathrm{2}} −\pi^{\mathrm{2}} \right)}{\mathrm{36}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\bigstar \\ $$
Commented by Dwaipayan Shikari last updated on 18/Mar/21

$$ \\ $$😃
Commented by Ajetunmobi last updated on 18/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{did}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{same}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{mine}}\: \\ $$$$\boldsymbol{\mathrm{but}}\:\boldsymbol{\mathrm{why}}? \\ $$
Commented by Ar Brandon last updated on 18/Mar/21

$$\mathrm{Because}\:\mathrm{I}\:\mathrm{wanna}\:\mathrm{learn}\:\mathrm{from}\:\mathrm{you}\:\mathrm{too}. \\ $$$$\mathrm{Just}\:\mathrm{as}\:\mathrm{I}\:\mathrm{do}\:\mathrm{with}\:\mathrm{the}\:\mathrm{other}\:\mathrm{members}. \\ $$😄😇
Commented by Ajetunmobi last updated on 18/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{ok}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{learnig}}\:\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{each}}\: \\ $$$$\boldsymbol{\mathrm{other}} \\ $$
Commented by Ar Brandon last updated on 18/Mar/21

😀
Commented by SLVR last updated on 13/Apr/21
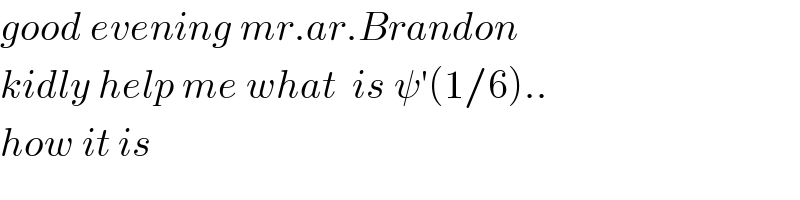
$${good}\:{evening}\:{mr}.{ar}.{Brandon}\: \\ $$$${kidly}\:{help}\:{me}\:{what}\:\:{is}\:\psi'\left(\mathrm{1}/\mathrm{6}\right).. \\ $$$${how}\:{it}\:{is} \\ $$
